题目内容
6.已知函数f(x)=$\left\{{\begin{array}{l}{{3^x},x≤0}\\{{{log}_2}x,x>0}\end{array}}\right.$,若f(x0)>0,则x0的取值范围是x0>1或x0≤0.分析 根据分段函数的表达式进行,分别求解即可.
解答 解:若x0≤0,则由f(x0)>0得${3}^{{x}_{0}}$>0,此时不等式恒成立,
若x0>0,则由f(x0)>0得log2x0>0,得x0>1,
综上x0>1或x0≤0,
故答案为:x0>1或x0≤0
点评 本题主要考查不等式的求解,根据分段函数的表达式的表达式分别进行求解是解决本题的关键.

练习册系列答案
 世纪百通期末金卷系列答案
世纪百通期末金卷系列答案
相关题目
1.某校食堂使用大小、手感完全一样的餐票,小明口袋里有一元餐票2张,两元餐票3张,五元餐票1张,若从他口袋中随意摸出2张,则其面值之和不少于4元的概率为( )
| A. | $\frac{7}{15}$ | B. | $\frac{8}{15}$ | C. | $\frac{3}{5}$ | D. | $\frac{2}{3}$ |
16.已知函数f(x)=$\left\{\begin{array}{l}{{2}^{x}-2,x≤0}\\{-lo{g}_{3}x,x>0}\end{array}\right.$,且f(a)=-2,则f(7-a)=( )
| A. | -$\frac{7}{4}$ | B. | -$\frac{5}{4}$ | C. | -$\frac{3}{4}$ | D. | -log37 |
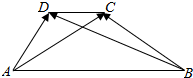 如图,梯形ABCD中,AB∥CD,AB=3CD.
如图,梯形ABCD中,AB∥CD,AB=3CD.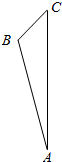 在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].
在△ABC中,∠BAC=10°,∠ACB=30°,将直线BC绕AC旋转得到B1C,直线AC绕AB旋转得到AC1,则在所有旋转过程中,直线B1C与直线AC1所成角的取值范围为[10°,50°].