题目内容
3.已知函数f(x)=|$\frac{1}{x}$-1|.(1)画出函数f(x)的图象,并写出其单调区间;
(2)当x∈[$\frac{1}{2}$,2],求函数y=f(x)的值域;
(3)是否存在实数a,b(0<a<b),使当x∈[a,b]时,f(x)的值域为[$\frac{a}{6}$,$\frac{b}{6}$],若存在,求出a,b的值,若不存在,说明理由.
分析 (1)去绝对值号得到$f(x)=\left\{\begin{array}{l}{\frac{1}{x}-1}&{0<x≤1}\\{-\frac{1}{x}+1}&{x<0,或x>1}\end{array}\right.$,根据反比例函数$y=\frac{1}{x}$和$y=-\frac{1}{x}$的图象即可画出该函数的图象,从而根据图象即可得出f(x)的单调区间;
(2)根据图象即知f(x)在$[\frac{1}{2},2]$上的最小值为0,再比较端点值便可求出其最大值,从而得出值域;
(3)分0<b≤1,0<a<1<b,和a≥1这三种情况,根据f(x)的单调性及取得最小值0的情况求出每种情况下的f(x)在[a,b]的值域,根据f(x)的值域为$[\frac{a}{6},\frac{b}{6}]$,便可求出a,b,并判断求得的a,b是否符合条件.
解答 解:(1)$f(x)=|\frac{1}{x}-1|=\left\{\begin{array}{l}{\frac{1}{x}-1}&{0<x≤1}\\{-\frac{1}{x}+1}&{x<0,或x>1}\end{array}\right.$,f(x)的图象可以由反比例函数的图象平移得到,图象如下: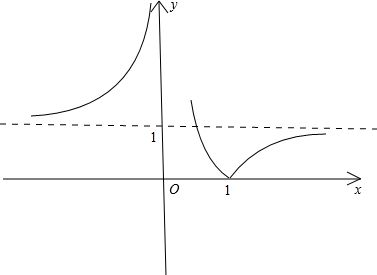 由图象可以看出f(x)的单调增区间为:(-∞,0),(1,+∞),单调减区间为:(0,1];
由图象可以看出f(x)的单调增区间为:(-∞,0),(1,+∞),单调减区间为:(0,1];
(2)由图象可以看出x$∈[\frac{1}{2},2]$时,最小值为f(1)=0,$f(\frac{1}{2})=1,f(2)=\frac{1}{2}$;
∴f(x)在[$\frac{1}{2},2$]上的值域为[0,1];
(3)①若0<b≤1,$f(x)=\frac{1}{x}-1$,则f(x)在[a,b]上单调递减;
∴f(x)∈[f(b),f(a)]=$[\frac{1}{b}-1,\frac{1}{a}-1]$;
又f(x)在[a,b]上的值域为$[\frac{a}{6},\frac{b}{6}]$;
$\left\{\begin{array}{l}{\frac{1}{b}-1=\frac{a}{6}}\\{\frac{1}{a}-1=\frac{b}{6}}\end{array}\right.$;
解得b=0,与b>0矛盾,∴这种情况不存在;
②若0<a<1<b,则:
f(x)在[a,b]上的最小值为0;
∴$\frac{a}{6}=0$,a=0与a>0矛盾,∴这种情况不存在;
③若a≥1,则f(x)在[a,b]上单调递增;
∴$f(x)∈[f(a),f(b)]=[-\frac{1}{a}+1,-\frac{1}{b}+1]$;
∴$\left\{\begin{array}{l}{-\frac{1}{a}+1=\frac{a}{6}}\\{-\frac{1}{b}+1=\frac{b}{6}}\end{array}\right.$;
解得$\left\{\begin{array}{l}{a=2}\\{b=3}\end{array}\right.$,或$\left\{\begin{array}{l}{a=3}\\{b=2}\end{array}\right.$(舍去);
∴存在实数a,b(0<a<b),使当x∈[a,b]时,f(x)的值域为$[\frac{a}{6},\frac{b}{6}]$,此时a=2,b=3.
点评 考查含绝对值函数的处理方法:去绝对值号,反比例函数的图象,图象的平移,以及根据图象写出函数的单调区间,根据图象求函数的值域,根据单调性定义求函数的值域.

 阅读快车系列答案
阅读快车系列答案| A. | -$\frac{3}{2}$b2 | B. | $\frac{3}{2}$b2 | C. | -$\frac{3}{2}$b${\;}^{\frac{7}{3}}$ | D. | $\frac{3}{2}$b${\;}^{\frac{7}{3}}$ |