题目内容
设数列1,1+2,1+2+3,…的前n项的和为Sn,则Sn等于( )
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:数列的求和
专题:等差数列与等比数列
分析:由an=1+2+3+…+n=
(n2+n),得Sn=
[(1+2+3+…+n)+(12+22+32+…+n2)],由此能求出Sn.
| 1 |
| 2 |
| 1 |
| 2 |
解答:
解:∵an=1+2+3+…+n=
=
(n2+n),
∴Sn=
[(1+2+3+…+n)+(12+22+32+…+n2)]
=
[
+
]
=
.
故选:A.
| n(n+1) |
| 2 |
| 1 |
| 2 |
∴Sn=
| 1 |
| 2 |
=
| 1 |
| 2 |
| n(n+1) |
| 2 |
| n(n+1)(2n+1) |
| 6 |
=
| n(n+1)(n+2) |
| 6 |
故选:A.
点评:本题考查数列的前n项和的求法,是中档题,解题时要认真审题,注意分组求和法的合理运用.

练习册系列答案
相关题目
不等式2x3-7x2-4x<0的解为( )
A、x<-
| ||
B、-
| ||
C、-
| ||
| D、无解 |
下列说法正确的是( )
| A、命题“若x=2,则x2=4”的否命题为“若x2≠4,则x≠2” |
| B、命题“?x∈R,x2+x-1<0”的否定是“?x∈R,x2+x-1>0” |
| C、“x=y”是“sinx=siny”的充分不必要条件 |
| D、命题“若x=0或y=0,则xy=0”的逆否命题为“若xy≠0,则x≠0或y≠0” |
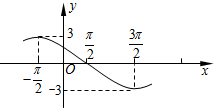 已知函数f(x)=Acos(ωx+φ) (A>0,ω>0,|φ|<
已知函数f(x)=Acos(ωx+φ) (A>0,ω>0,|φ|<