题目内容
11.已知个面向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{21}$,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,则|$\overrightarrow{b}$|=2.分析 利用已知等式以及平面向量的数量积得到关于|$\overrightarrow{b}$|的方程解之.
解答 解:向量$\overrightarrow{a}$,$\overrightarrow{b}$满足|$\overrightarrow{a}$|=1,|$\overrightarrow{a}$-2$\overrightarrow{b}$|=$\sqrt{21}$,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,
所以|$\overrightarrow{a}$-2$\overrightarrow{b}$|2=21,且$\overrightarrow{a}$与$\overrightarrow{b}$夹角为120°,则${\overrightarrow{a}}^{2}+4{\overrightarrow{b}}^{2}-4|\overrightarrow{a}||\overrightarrow{b}|cos120°=21$,整理得$2|\overrightarrow{b}{|}^{2}+|\overrightarrow{b}|-10=0$,解得|$\overrightarrow{b}$|=2;
故答案为:2.
点评 本题考查了平面向量的模长以及数量积的运算;属于基础题.

练习册系列答案
相关题目
9.已知F是双曲线E:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1$(a>0,b>0)的右焦点,过点F作E的一条渐近线的垂线,垂足为P,垂线PF与E相交于点Q,记点Q到E的两条渐近线的距离之积为d2,若|FP|=2d,则该双曲线的离心率( )
| A. | $\sqrt{2}$ | B. | 2 | C. | 3 | D. | 4 |
6.已知条件p:log2(x-1)<1的解,q:x2-2x-3<0的解,则p是q的( )条件.
| A. | 充分非必要 | B. | 必要非充分 | ||
| C. | 充分必要 | D. | 既非充分又非必要 |
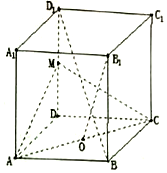 在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.
在正方体ABCD-A1B1C1D1中,M为DD1的中点,O为AC的中点,AB=1.