题目内容
设定义域为R的函数f(x)=
若函数g(x)=f2(x)-(2m+1)•f(x)+m2有7个零点,则实数m的值为( )
|
| A、0 | B、6 | C、2或6 | D、2 |
考点:分段函数的应用
专题:函数的性质及应用
分析:作出函数f(x)的图象,根据g(x)的零点个数分别进行判断即可得到结论.
解答:
解:作出函数的图象如图: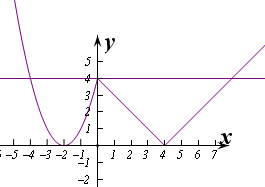
当m=0时,f(x)=0或f(x)=1,f(x)=0有2个不同实根,f(x)=1有4个不同实根,不符合题意;
当m=6时,f(x)=4或f(x)=9,f(x)=4
有3个不同实根,f(x)=9有2个不同实根,不符合题意;
当m=2时,f(x)=1或f(x)=4,得到f(x)=1有4个不同实根,f(x)=4有3个不同实根,符合题意.
故选D.

当m=0时,f(x)=0或f(x)=1,f(x)=0有2个不同实根,f(x)=1有4个不同实根,不符合题意;
当m=6时,f(x)=4或f(x)=9,f(x)=4
有3个不同实根,f(x)=9有2个不同实根,不符合题意;
当m=2时,f(x)=1或f(x)=4,得到f(x)=1有4个不同实根,f(x)=4有3个不同实根,符合题意.
故选D.
点评:本题主要考查函数零点的应用,利用数形结合是解决本题的关键.难度较大.

练习册系列答案
相关题目
已知tan(x+
)=
,0<x<
,则
=( )
| π |
| 4 |
| 12 |
| 5 |
| π |
| 4 |
| cos2x | ||
sin(
|
A、
| ||
B、
| ||
C、
| ||
D、-
|
设f0(x)=sinx,f1(x)=f0′(x),f2(x)=f1′(x),…,fn+1(x)=fn′(x),n∈N,则f2015(x)=( )
| A、sinx | B、-sinx |
| C、cosx | D、-cosx |
设
=(sin25°,cos25°),
=(cos25°,sin25°),则
与
的夹角是( )
| a |
| b |
| a |
| b |
| A、50° | B、40° |
| C、90° | D、0° |
cos
的值为( )
| 23π |
| 6 |
A、-
| ||||
B、-
| ||||
C、
| ||||
D、
|
设数列{an}是等差数列,且a4=-5,a9=5,Sn是an的前n项和,则( )
| A、S7=S5 |
| B、S5<S6 |
| C、S5=S6 |
| D、S7=S6 |
已知函数f(x)定义域为R,对于定义域内任意x、y,都有f(x)+f(y)=f(x+y),且x>0时,f(x)<0,则( )
| A、f(x)是偶函数且在(-∞,+∞)上单调递减 |
| B、f(x)是偶函数且在(-∞,+∞)上单调递增 |
| C、f(x)是奇函数且在(-∞,+∞)上单调递减 |
| D、f(x)是奇函数且在(-∞,+∞)上单调递增 |
要得到函数y=
cos(x-
)的图象,可把函数y=sinx+cosx的图象( )
| 2 |
| π |
| 6 |
A、向左平移
| ||
B、向右平移
| ||
C、向左平移
| ||
D、向右平移
|
