题目内容
12.已知$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为$\frac{π}{3}$,那么$|{\overrightarrow a+3\overrightarrow b}|$等于( )| A. | $\sqrt{7}$ | B. | $\sqrt{10}$ | C. | 4 | D. | $\sqrt{13}$ |
分析 根据平面向量数量积的定义计算模长即可.
解答 解:$\overrightarrow a,\overrightarrow b$均为单位向量,它们的夹角为$\frac{π}{3}$,
所以${(\overrightarrow{a}+3\overrightarrow{b})}^{2}$=${\overrightarrow{a}}^{2}$+6$\overrightarrow{a}$•$\overrightarrow{b}$+9${\overrightarrow{b}}^{2}$=12+6×1×1×cos$\frac{π}{3}$+9×12=13,
那么$|{\overrightarrow a+3\overrightarrow b}|$=$\sqrt{13}$.
故选:D.
点评 本题考查了平面向量数量积的定义与应用问题,是基础题目.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
7.设$\overrightarrow a=(-3,m),\overrightarrow b=(4,3)$,若$\overrightarrow a$与$\overrightarrow b$的夹角是钝角,则实数m的范围是( )
| A. | m>4 | B. | m<4 | C. | m<4且$m≠\frac{9}{4}$ | D. | m<4且$m≠-\frac{9}{4}$ |
4.已知函数f(x)的图象是连续不断的,有如下的x,f(x)对应值表:
那么函数f(x)在区间[1,6]上的零点至少有( )
| x | 1 | 2 | 3 | 4 | 5 | 6 | 7 |
| f(x) | 123.5 | 21.5 | -7.82 | 11.57 | -53.7 | -126.7 | -129.6 |
| A. | 5个 | B. | 4个 | C. | 3个 | D. | 2个 |
1.某农户计划种植黄瓜和冬瓜,种植面积不超过50亩,投入资金不超过54万元,假设种植黄瓜与冬瓜的产量、成本和售价如表:
为使一年的种植总利润(总利润=总销售收入-总种植成本)最大,那么黄瓜与冬瓜的种植面积(单位:亩)分别为( )
| 年产量/亩 | 年种植成本/亩 | 每吨售价 | |
| 黄瓜 | 4吨 | 1.2万元 | 0.55万元 |
| 冬瓜 | 6吨 | 0.9万元 | 0.3万元 |
| A. | 50,0 | B. | 30,20 | C. | 20,30 | D. | 0,50 |
2.已知函数f(x)=|x2+bx|(b∈R),当x∈[0,1]时,f(x)的最大值为M(b),则M(b)的最小值是( )
| A. | 3-2$\sqrt{2}$ | B. | 4-2$\sqrt{3}$ | C. | 1 | D. | 5-2$\sqrt{5}$ |
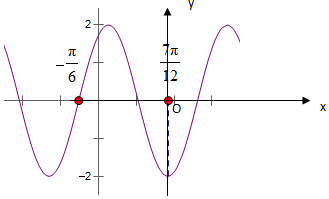 已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.
已知f(x)=Asin(ωx+φ)(A>0,ω>0,-π<φ<π)的图象如图所示.