题目内容
3.已知正三棱柱ABC-A1B1C1的各棱长都为1,M是底面BC边上的中点,N是侧棱CC1上的点,且$CN=\frac{1}{4}C{C_1}$,则AB1与MN所成的角是$\frac{π}{2}$.分析 取AC中点O,A1C1中点D,以O为原点,OB为x轴,OC为y轴,OD为z轴,建立空间直角坐标系,利用向量法能求出AB1与MN所成的角的大小.
解答 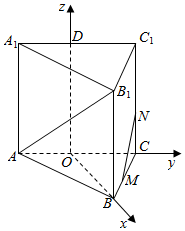 解:取AC中点O,A1C1中点D,
解:取AC中点O,A1C1中点D,
以O为原点,OB为x轴,OC为y轴,OD为z轴,建立空间直角坐标系,
∵正三棱柱ABC-A1B1C1的各棱长都为1,M是底面BC边上的中点,N是侧棱CC1上的点,且$CN=\frac{1}{4}C{C_1}$,
∴A((0,-$\frac{1}{2}$,0),B1($\frac{\sqrt{3}}{2}$,0,1),M($\frac{\sqrt{3}}{4}$,$\frac{1}{4}$,0),N(0,$\frac{1}{2}$,$\frac{1}{4}$),
$\overrightarrow{A{B}_{1}}$=($\frac{\sqrt{3}}{2}$,$\frac{1}{2}$,1),$\overrightarrow{MN}$=(-$\frac{\sqrt{3}}{4}$,$\frac{1}{4}$,$\frac{1}{4}$),
∴$\overrightarrow{A{B}_{1}}•\overrightarrow{MN}$=-$\frac{3}{8}+\frac{1}{8}+\frac{1}{4}$=0.
∴AB1与MN所成的角是$\frac{π}{2}$.
故答案为:$\frac{π}{2}$.
点评 本题考查空间中两条异面直线所成角的大小的求法,是中档题,解题时要认真审题,注意向量法的合理运用.

练习册系列答案
相关题目
11.已知l、m、n是空间不同的三条直线,则下列结论中正确的( )
| A. | 若m⊥l,n⊥l,则m⊥n | B. | 若m⊥l,n⊥l,则m∥n | C. | 若m⊥l,n∥l,则m⊥n | D. | 若m⊥l,n∥l,则m∥n |
18.如图,空间四边形ABCD中,“AC=AD”“BC=BD”则AB与CD所成的角为( )
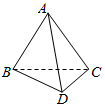

| A. | 30° | B. | 45° | C. | 60° | D. | 90° |
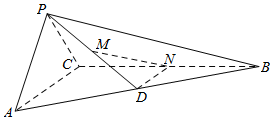 在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.
在三棱锥P-ABC中,平面PAC⊥平面ABC,PA⊥PC,AC⊥BC,D为AB的中点,M为PD的中点,N在棱BC上.