题目内容
设f(x)是定义在区间(a,b)上的函数,若对?x1,x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,则称y=f(x)是区间(a,b)上的“温和函数”,下列函数不是其定义域上的“温和函数”的是( )
| A、f(x)=x2-x,x∈(-1,1) |
| B、f(x)=sinx,x∈R |
| C、f(x)=ex,x∈(-∞,0) |
| D、f(x)=lnx,x∈(1,+∞) |
考点:函数与方程的综合运用
专题:函数的性质及应用
分析:利用新定义,判断表达式的几何意义,通过函数的导数求出函数的斜率的范围,推出结果即可.
解答:
解:设f(x)是定义在区间(a,b)上的函数,若对?x1,x2∈(a,b),都有|f(x1)-f(x2)|≤|x1-x2|,可得|
|≤1,即函数图象上任意两点的连线的斜率的绝对值小于等于1.则称y=f(x)是区间(a,b)上的“温和函数”,
因为f(x)=x2-x,x∈(-1,1),f′(x)=2x-1,x∈(-1,1)时,f′(x)∈(-3,1),不满足|f(x1)-f(x2)|≤|x1-x2|,因此f(x)=x2-x,x∈(-1,1),不是x∈(-1,1),上的“温和函数”;
f(x)=sinx,x∈R,可得f′(x)=cosx∈[-1,1].满足新定义.
f(x)=ex,x∈(-∞,0),f′(x)=ex∈(0,1),满足新定义.
f(x)=lnx,x∈(1,+∞),f′(x)=
∈(0,1).满足新定义.
故选:A.
| f(x1)-f(x2) |
| x1-x2 |
因为f(x)=x2-x,x∈(-1,1),f′(x)=2x-1,x∈(-1,1)时,f′(x)∈(-3,1),不满足|f(x1)-f(x2)|≤|x1-x2|,因此f(x)=x2-x,x∈(-1,1),不是x∈(-1,1),上的“温和函数”;
f(x)=sinx,x∈R,可得f′(x)=cosx∈[-1,1].满足新定义.
f(x)=ex,x∈(-∞,0),f′(x)=ex∈(0,1),满足新定义.
f(x)=lnx,x∈(1,+∞),f′(x)=
| 1 |
| x |
故选:A.
点评:本题考查函数与方程的综合应用,考查新定义的理解,学生分析解决问题的能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
x2=49的充分必要条件是( )
| A、x=7 |
| B、x=-7 |
| C、x=7或x=-7 |
| D、x=7且x=-7 |
在3与27之间插入7个数,使它们成为等差数列,则插入的7个数的第四个数是( )
| A、18 | B、9 | C、12 | D、15 |
如图所示,在平行六面体ABCD-A1B1C1D1中,点E为上底面对角线A1C1的中点,若
=
+x
+y
,则( )
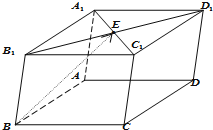
| BE |
| AA1 |
| AB |
| AD |

A、x=-
| ||||
B、x=
| ||||
C、x=-
| ||||
D、x=
|
 如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且
如图,平面直角坐标系中,动点P(x,y),PM⊥y轴,垂足为M,点N与点P关于x轴对称,且