题目内容
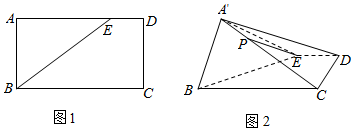
20.如图1,在矩形ABCD中,AB=$\sqrt{3}$,BC=4,E是边AD上一点,且AE=3,把△ABE沿BE翻折,使得点A到A′,满足平面A′BE与平面BCDE垂直(如图2).(1)若点P在棱A′C上,且CP=3PA′,求证:DP∥平面A′BE;
(2)求二面角B-A′E-D的余弦值的大小.
分析 (1)若点P在棱A′C上,且CP=3PA′,根据线面平行的判定定理即可证明DP∥平面A′BE;
(2)建立空间坐标系,求出平面的法向量,利用向量法即可求二面角B-A′E-D的余弦值的大小.
解答 解:(1)在图2中,过P作PQ∥BC交A'B于Q.…(1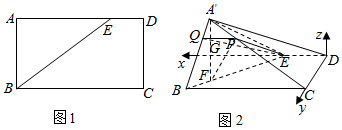
∵CP=3PA',∴$\frac{PQ}{BC}=\frac{A'P}{A'C}=\frac{1}{4}$,
∵BC=4,∴PQ=1,…(2分)
∵DE∥BC.DE=1,
∴$DE\underline{\underline{∥}}PQ$,
得DE∥QP.∴DP∥EQ…(4分)
∵DP?平面A'BE,EQ?平面A'BE∴DP∥平面A'BE.…(5分)
(2)在图2中,过A'作A'F⊥BE于F.
∵平面A'BE⊥平面BCDE,
∴A'F⊥平面BCDE …(6分)
∵∠BA′E=90°,A′B=$\sqrt{3}$,A′E=3,
∴∠A'EB=30°,A′F=$\frac{3}{2}$,EF=$\frac{3\sqrt{3}}{2}$,
过F作FG⊥DE交DE延长线于G,则FG=$\frac{3\sqrt{3}}{4}$,EG=$\frac{9}{4}$…(7分)
如图,建立空间直角坐标系D-xyz,$\overrightarrow{EA'}=(\frac{9}{4},\frac{{3\sqrt{3}}}{4},\frac{3}{2})$,$\overrightarrow{EF}$=($\frac{9}{4}$,$\frac{3\sqrt{3}}{4}$,0),$\overrightarrow{DE}$=(1,0,0)…(8分)
设平面A'BE的法向量$\overrightarrow n=(x,y,z)$,则$\left\{\begin{array}{l}{\frac{9}{4}x+\frac{3\sqrt{3}}{4}y=0}\\{\frac{9}{4}x+\frac{3\sqrt{3}}{4}y+\frac{3}{2}z=0}\end{array}\right.$,可取$\overrightarrow n=(1,-\sqrt{3},0)$ …(9分)
设平面A'DE的法向量$\overrightarrow m=({x_1},{y_1},{z_1})$,则$\left\{\begin{array}{l}{{x}_{1}=0}\\{\frac{9}{4}{x}_{1}+\frac{3\sqrt{3}}{4}{y}_{1}+\frac{3}{2}{z}_{1}=0}\end{array}\right.$,可取$\overrightarrow m=(0,2,-\sqrt{3})$ …(10分),
∴$cos<\overrightarrow m,\overrightarrow n>=\frac{{-2\sqrt{3}}}{{\sqrt{1+3}•\sqrt{4+3}}}=-\frac{{\sqrt{21}}}{7}$ …(11分)
∵二面角B-A'E-D为钝角,
∴二面角B-A'E-D的余弦的大小为$-\frac{{\sqrt{21}}}{7}$. …(12分)
点评 本题主要考查直线和平面平行的判定以及二面角的求解,利用线面平行的判定定理以及建立坐标系,利用向量法是解决本题的关键.综合性较强,运算量较大.

 全优测试卷系列答案
全优测试卷系列答案 冲刺100分1号卷系列答案
冲刺100分1号卷系列答案| A. | 1 | B. | 4 | C. | -1 | D. | -4 |
| A. | $\frac{1}{2}$ | B. | 1 | C. | 2 | D. | 4 |
| A. | y=x3 | B. | y=|x+1| | C. | y=-x2 | D. | y=|x|+1 |
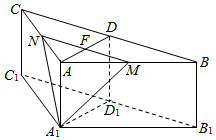 如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N.
如图,在三棱柱ABC-A1B1C中,侧棱AA1⊥底面ABC,AB=AC=2AA1,∠BAC=120°,D,D1 分别是线段BC,B1C1的中点,过线段AD的中点P作BC的平行线,分别交AB,AC于点M,N. 函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$).
函数f(x)=2sin(ωx+φ)(ω>0,-$\frac{π}{2}$<φ<$\frac{π}{2}$)的部分图象如图所示,则函数f(x)解析式f(x)=2sin(2x-$\frac{π}{3}$). 如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).
如图(1),在Rt△ABC中,∠C=90°,BC=3,AC=6,D,E分别是AC,AB上的点,且DE∥BC,DE=2,将△ADE沿DE折起到△A1DE的位置,使A1C⊥CD,如图(2).