题目内容
15．已知幂函数y=f（x）图象过点（9，3），则${∫}_{0}^{1}$f（x）dx等于$\frac{2}{3}$．分析 根据根据幂函数f（x）=xn可求得n的值，再求定积分的值．
解答 解：设f（x）=xn，则${9}^{n}=\frac{1}{3}$则$n=\frac{1}{2}$，
∴${∫}_{0}^{1}$f（x）dx=${∫}_{0}^{\frac{1}{2}}{x}^{\frac{1}{2}}$dx=$\frac{2}{3}{x}^{\frac{3}{2}}{丨}_{0}^{1}$=$\frac{2}{3}$，
故答案为：$\frac{2}{3}$
点评 本题考查求幂函数的解析式和定积分的内容，属于基础题．
练习册系列答案
相关题目
3．函数f（x）=sinx+tanx，则使不等式f（sinθ）+f（cosθ）≥0成立的θ取值范围是（ ）
| A． | [2kπ+$\frac{π}{4}$，2kπ+$\frac{5π}{4}$]（k∈Z） | B． | [2kπ-$\frac{3π}{4}$，2kπ+$\frac{π}{4}$]（k∈Z） | ||
| C． | [2kπ-$\frac{π}{4}$，2kπ+$\frac{3π}{4}$]（k∈Z） | D． | [2kπ+$\frac{3π}{4}$，2kπ+$\frac{7π}{4}$]（k∈Z） |
如图，直角梯形ABCD与等腰直角三角形ABE所在的平面互相垂直．AB∥CD，AB⊥BC，AB=2CD=2BC，EA⊥EB．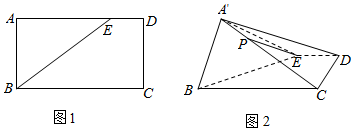
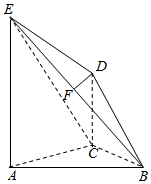在如图所示的几何体中，平面ACDE⊥平面ABC，CD∥AE，F是BE的中点，∠ACB=90°，AE=2CD=2，AC=BC=1，BE=$\sqrt{6}$．