题目内容
14.已知直线L与抛物线C:y2=4x交于A、B两点,且线段AB的中点M(3,2).(Ⅰ)求直线L的方程
(Ⅱ)线段AB的长.
分析 (Ⅰ)直线L:y-2=k(x-3),直线方程与抛物线方程联立化为:k2x2-6kx+(2-3k)2=0,根据线段AB的中点M(3,2),即可求出k的值,
(Ⅱ)设A(x1,y1),B(x2,y2),x1+x2=6,利用|AB|=x1+x2+p即可得出.
解答 解:(Ⅰ)设直线L:y-2=k(x-3),
由$\left\{\begin{array}{l}y-2=k(x-3)\\{y^2}=4x\end{array}\right.$消去y整理得,k2x2-6kx+(2-3k)2=0
当k=0时,显然不成立.
当k≠0时.${x_1}+{x_2}=\frac{6}{k}$,
又$\frac{{{x_1}+{x_2}}}{2}=3$得,$\frac{6}{k}=6,k=1$,
∴直线L:y-2=x-3,即x-y-1=0;
(Ⅱ)又焦点F(1,0)满足直线L:x-y-1=0.
设A(x1,y1),B(x2,y2),
又|AB|=|FA|+|FB|=(x1+1)+(x2+1),
x1+x2=6,
∴|AB|=8.
点评 本题考查了抛物线的定义标准方程及其性质、直线与抛物线相交弦长问题,考查了推理能力与计算能力,属于中档题.

练习册系列答案
 开心试卷期末冲刺100分系列答案
开心试卷期末冲刺100分系列答案 双基同步导航训练系列答案
双基同步导航训练系列答案
相关题目
4.已知平面向量$\overrightarrow{a}$,$\overrightarrow{b}$的夹角为$\frac{π}{3}$,且|$\overrightarrow{a}$|=1,|$\overrightarrow{b}$|=$\frac{1}{2}$,则$\overrightarrow{a}$+2$\overrightarrow{b}$与$\overrightarrow{b}$的夹角是( )
| A. | $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{4}$ | D. | $\frac{3π}{4}$ |
5.已知z是复数,且$\frac{z+2}{i}$=1+i,则z在复平面内对应的点的坐标为( )
| A. | (-3,1) | B. | (-3,-1) | C. | (1,-3) | D. | (-1,-3) |
9.椭圆$\frac{x^2}{4}+\frac{y^2}{3}=1$的左、右焦点分别为F1、F2,过F2作x轴的垂线交椭圆于点P,过P与原点O的直线交椭圆于另一点Q,则△F1PQ的周长为( )
| A. | 4 | B. | 8 | C. | $4+\sqrt{13}$ | D. | $2+\sqrt{13}$ |
19.在△ABC中,a,b,c分别是角A,B,C所对的边,且$a=2,b=\sqrt{2},A=\frac{π}{4}$,则角B=( )
| A. | $\frac{5π}{6}$或 $\frac{π}{6}$ | B. | $\frac{5π}{6}$ | C. | $\frac{π}{3}$ | D. | $\frac{π}{6}$ |
 如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.
如图,已知△ABC内接于⊙O,连结AO并延长交⊙O于点D,∠ACB=∠ADC.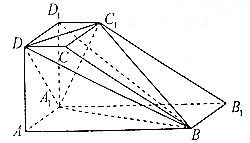 如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.
如图,直四棱柱ABCD-A1B1C1D1的底面ABCD是直角梯形,其中AB⊥AD,AB=2AD=2AA1=4,CD=1.