题目内容
已知椭圆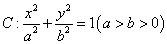 ,其中
,其中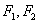 为左、右焦点,O为坐标原点.直线l与椭圆交于
为左、右焦点,O为坐标原点.直线l与椭圆交于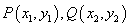 两个不同点.当直线l过椭圆C右焦点F2且倾斜角为
两个不同点.当直线l过椭圆C右焦点F2且倾斜角为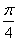 时,原点O到直线l的距离为
时,原点O到直线l的距离为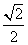 .又椭圆上的点到焦点F2的最近距离为
.又椭圆上的点到焦点F2的最近距离为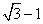 .
.
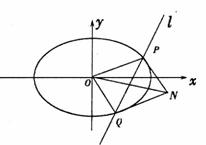
(I)求椭圆C的方程;
(II)以OP,OQ为邻边做平行四边形OQNP,当平行四边形OQNP面积为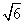 时,求平行四边形OQNP的对角线之积
时,求平行四边形OQNP的对角线之积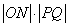 的最大值;
的最大值;
(III)若抛物线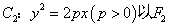 为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
为焦点,在抛物线C2上任取一点S(S不是原点O),以OS为直径作圆,交抛物线C2于另一点R,求该圆面积最小时点S的坐标.
解析:(Ⅰ)直线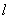 的倾斜角为
的倾斜角为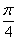 ,
,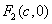 ,直线
,直线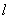 的方程
的方程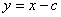 ,
,
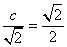 ,
,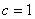 ,
,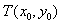 为椭圆
为椭圆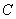 上任一点,
上任一点,
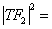
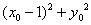 =
=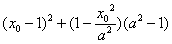 =
=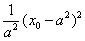 ≥
≥ ,
,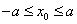 ,
,
当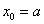 时,
时,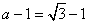 ,
,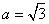 ,
,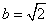 ,
,
椭圆 的方程
的方程 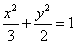 ..………………………5分
..………………………5分
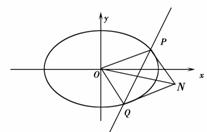
(Ⅱ)当直线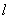 的斜率不存在时,
的斜率不存在时,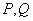 两点关于
两点关于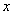 轴对称,则
轴对称,则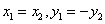 ,
,
由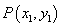 在椭圆上,则
在椭圆上,则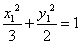 ,而
,而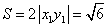 ,则
,则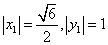 ,
,
知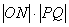 =
=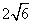 .
.
当直线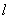 的斜率存在时,设直线
的斜率存在时,设直线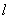 为
为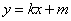 ,代入
,代入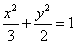 可得
可得
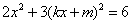 ,
,
即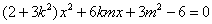 ,
,
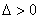 ,即
,即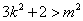 ,
,
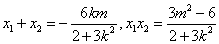 ,
,
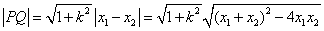
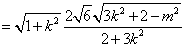 ,
,
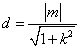 ,
,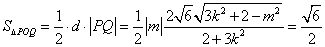 ,
,
化为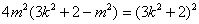 ,
,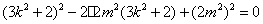 ,
,
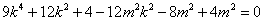 ,
,
得到,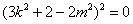 ,则
,则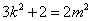 ,满足
,满足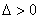 ,
,
由前知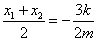 ,
,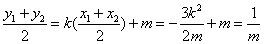 ,
,
设M是ON与PQ的交点,则
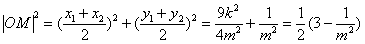 ,
,
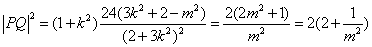 ,
,
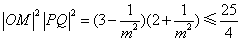 ,当且仅当
,当且仅当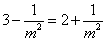 ,
,
即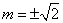 时等号成立,
时等号成立,
综上可知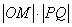 的最大值为
的最大值为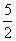 .
.
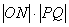 =2
=2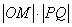 的最大值为5.………………………10分
的最大值为5.………………………10分
(Ⅲ)因为以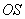 为直径的圆与
为直径的圆与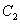 相交于点
相交于点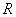 ,所以∠ORS = 90°,即
,所以∠ORS = 90°,即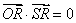 ,
,
设S (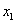 ,
,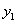 ),R(
),R(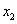 ,
,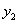 ),
),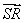 =(
=(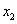 -
-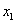 ,
,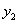 -
-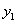 ),
),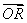 =(
=(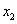 ,
,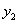 ),
),
所以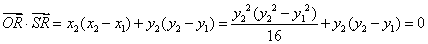 ,
,
因为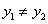 ,
,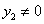 ,化简得
,化简得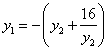 ,
,
所以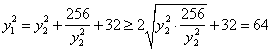 ,
,
当且仅当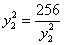 即
即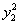 =16,y2=±4时等号成立.
=16,y2=±4时等号成立.
圆的直径|OS|=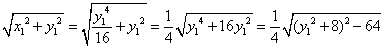 ,
,
因为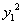 ≥64,所以当
≥64,所以当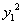 =64即
=64即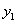 =±8时,
=±8时,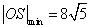 ,
,
所以所求圆的面积的最小时,点S的坐标为(16,±8)..

练习册系列答案
 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目
 于D,若AD=1,
于D,若AD=1, ,则圆O的面积是 .
,则圆O的面积是 .
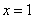 是函数
是函数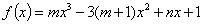 的一个极值点,其中
的一个极值点,其中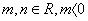
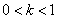 ),BD=l为定长,则△ABC的面积最大值为
),BD=l为定长,则△ABC的面积最大值为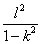 B.
B.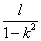 C.
C.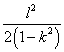 D.
D.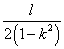
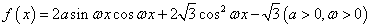 的最大值为2,且最小正周期为
的最大值为2,且最小正周期为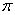 .
.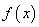 的解析式及其对称轴方程;
的解析式及其对称轴方程;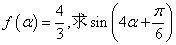 的值.
的值.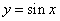 B.
B.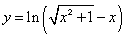
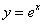 D.
D.
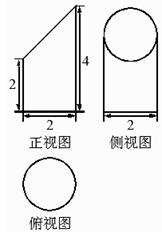
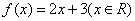 ,若
,若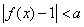 的必要条件是
的必要条件是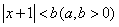 ,则
,则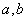 之间的关系是
之间的关系是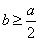 B.
B. C.
C.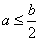 D.
D.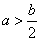
 , 则①处应填( )
, 则①处应填( )