题目内容
18.在等比数列{an}中,a1+a3=10,前4项和S4=30,则公比q等于2.分析 由题意和等比数列的前n项和公式、通项公式列出方程组,化简求出q的值.
解答 解:由题意得,$\left\{\begin{array}{l}{{a}_{1}+{a}_{1}{q}^{2}=10①}\\{{a}_{1}+{a}_{1}q+{a}_{1}{q}^{2}+{a}_{1}{q}^{3}=30②}\end{array}\right.$,
由①得${a}_{1}=\frac{10}{1+{q}^{2}}$,代入②化简得,
$\frac{10[(1+{q}^{2})+q(1+{q}^{2})]}{1+{q}^{2}}=30$,解得q=2,
故答案为:2.
点评 本题考查等比数列的前n项和公式、通项公式,以及方程思想的应用,属于基础题.

练习册系列答案
相关题目
10.设函数f(x)的定义域为R,且|f(x)|是偶函数,则下列结论中正确的是( )
| A. | f(x)是偶函数 | B. | f(x)是奇函数 | ||
| C. | |f(x-1)|的图象关于直线x=1对称 | D. | |f(x)+1|的图象关于点(0,1)对称 |
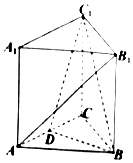 如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.
如图,在三棱柱ABC-A1B1C1中,AA1⊥平面ABC,△ABC为正三角形,AA1=AB=6,点D为AC的中点.