题目内容
8.已知直线l1:x-2y+5=0与直线l2:2x+my-6=0.(1)若两直线相互平行,求实数m的值;
(2)若两直线相互垂直,求实数m的值.
分析 (1)根据直线的平行关系求出m的值即可;(2)根据直线的垂直关系得到关于m的等式,求出m的值即可.
解答 解:(1)若两直线相互平行,
则$\frac{1}{-2}$=$\frac{2}{m}$,解得:m=-4;
(2)若两直线相互垂直,
则$\frac{1}{2}$×(-$\frac{2}{m}$)=-1,
∴m=1.
点评 本题考查了直线的平行和垂直关系,是一道基础题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
16.已知全集为R,M={x|x(x-3)<0},N={x|x<1或x≥3},则正确的为( )
| A. | M⊆N | B. | N⊆M | C. | ∁RN⊆M | D. | M⊆∁RN |
3.直线l与抛物线y2=6x交于A,B两点,圆(x-6)2+y2=r2与直线l相切于点M,且M为线段AB的中点.若这样的直线l恰有4条,则r的取值范围是( )
| A. | ($\sqrt{3}$,2$\sqrt{3}$) | B. | ($\sqrt{3}$,3$\sqrt{3}$) | C. | (3,$2\sqrt{3}$) | D. | (3,3$\sqrt{3}$) |
13.已知P是椭圆$\frac{{x}^{2}}{4}$+y2=1上的动点,则P点到直线l:x+y-2$\sqrt{5}$=0的距离的最小值为( )
| A. | $\frac{\sqrt{10}}{2}$ | B. | $\frac{\sqrt{5}}{2}$ | C. | $\frac{\sqrt{10}}{5}$ | D. | $\frac{\sqrt{2}}{5}$ |
17.已知$cos(\frac{π}{6}-x)=-\frac{{\sqrt{3}}}{3}$,则$cos(\frac{5π}{6}+x)+sin(\frac{2π}{3}-x)$=( )
| A. | $-\sqrt{3}$ | B. | -1 | C. | 0 | D. | $\sqrt{3}$ |
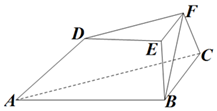 如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.
如图,在三棱台ABC-DEF中,平面BCFE⊥平面ABC,∠ACB=90°,BE=EF=FC=1,BC=2,AC=3.