题目内容
解关于x的不等式:
>a(a≥0).
| 1-a |
| x-1 |
考点:其他不等式的解法
专题:不等式的解法及应用
分析:根据题意,先将分式不等式转化为整式不等式,再对参数a分4类进行讨论,分别求出每种情况下的解集,综合即可得答案.
解答:
解:不等式可化为
<0,即(x-1)(ax-1)<0,
(1)若a=0,则不等式的解集是{x|x>1}.
(2)若a>0,则不等式可化为(x-1)(x-
)<0,
①当0<a<1时,1<
,不等式的解集为{x|1<x<
};
②当a>1时,1>
,不等式的解集为{x|
<x<1};
③当a=1时,不等式的解集为∅.
| ax-1 |
| x-1 |
(1)若a=0,则不等式的解集是{x|x>1}.
(2)若a>0,则不等式可化为(x-1)(x-
| 1 |
| a |
①当0<a<1时,1<
| 1 |
| a |
| 1 |
| a |
②当a>1时,1>
| 1 |
| a |
| 1 |
| a |
③当a=1时,不等式的解集为∅.
点评:本题考查分式不等式的解法,注意讨论参数a的取值范围,其中正确确定分类标准是关键.

练习册系列答案
相关题目
下列四组函数中,表示同一个函数的是( )
A、f(x)=x,g(x)=(
| |||
B、f(x)=x,g(x)=
| |||
C、f(x)=x,g(x)=
| |||
D、f(x)=x,g(x)=
|
 所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示,∠DAB=60°,CC1⊥A1C1.
所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示,∠DAB=60°,CC1⊥A1C1.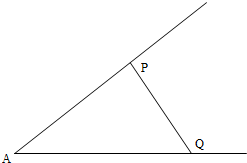 如图,已知锐角∠A为定角,点P,Q分别在∠A的两边上,且△APQ的面积为定值S,当P,Q在什么位置时,PQ长最短.
如图,已知锐角∠A为定角,点P,Q分别在∠A的两边上,且△APQ的面积为定值S,当P,Q在什么位置时,PQ长最短.