题目内容
如图所示,有一块边长为6m的正方形铁板,现从铁板的四个角各截去一个边长为x的小正方形,做成一个长方形的无盖容器.

(Ⅰ)求这个容器的容积V(x);
(Ⅱ)为使其容积V(x)最大,求截下的小正方形的边长x的值及容积V(x)的最大值.

(Ⅰ)求这个容器的容积V(x);
(Ⅱ)为使其容积V(x)最大,求截下的小正方形的边长x的值及容积V(x)的最大值.
考点:棱柱、棱锥、棱台的体积,基本不等式
专题:应用题,导数的综合应用
分析:(Ⅰ)无盖容器的底边长为6-2x,无盖容器的高为x,可得出容积V(x)与自变量x之间的关系式,由6-2x>0,可求出v(x)的定义域;
(Ⅱ)利用导数法,求出其函数值取最大值时,自变量x的值,即可得到要使无盖容器的容积最大,无盖容器的底边长.
(Ⅱ)利用导数法,求出其函数值取最大值时,自变量x的值,即可得到要使无盖容器的容积最大,无盖容器的底边长.
解答:
解:(Ⅰ)由题意,无盖容器的底边长为6-2x,无盖容器的高为x,
∴无盖容器的容积是V(x)与x的函数关系式是:V(x)=(6-2x)2•x,且f(x)的定义域为(0,3)
(Ⅱ)V′(x)=(6-2x)2•x=(6-2x)(6-6x),
令V′(x)=0,则x=1,或x=3(舍)
∵函数在(0,1)上单调递增,在(1,3)上单调递减
∴当无盖容器底面为1m时,无盖容器的容积最大为16m3.
∴无盖容器的容积是V(x)与x的函数关系式是:V(x)=(6-2x)2•x,且f(x)的定义域为(0,3)
(Ⅱ)V′(x)=(6-2x)2•x=(6-2x)(6-6x),
令V′(x)=0,则x=1,或x=3(舍)
∵函数在(0,1)上单调递增,在(1,3)上单调递减
∴当无盖容器底面为1m时,无盖容器的容积最大为16m3.
点评:本题考查函数模型的选择与应用,解题的关键是设出自变量并根据已知条件确定出函数的解析式和定义域,将一个实际问题转化为函数问题.

练习册系列答案
相关题目
a=-1是直线l1:ax+y=0与直线l2:x+ay+2=0平行的( )
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
 所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示,∠DAB=60°,CC1⊥A1C1.
所有棱长均为1的四棱柱ABCD-A1B1C1C1如图所示,∠DAB=60°,CC1⊥A1C1.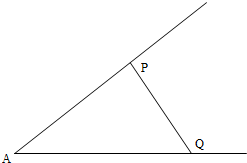 如图,已知锐角∠A为定角,点P,Q分别在∠A的两边上,且△APQ的面积为定值S,当P,Q在什么位置时,PQ长最短.
如图,已知锐角∠A为定角,点P,Q分别在∠A的两边上,且△APQ的面积为定值S,当P,Q在什么位置时,PQ长最短.