题目内容
3.若复数z满足z(1+i)2=1-i,其中i为虚数单位,则z在复平面内所对应的点位于( )| A. | 第一象限 | B. | 第二象限 | C. | 第三象限 | D. | 第四象限 |
分析 把已知等式变形,利用复数代数形式的乘除运算化简,求出z的坐标得答案.
解答 解:∵z(1+i)2=1-i,
∴$z=\frac{1-i}{(1+i)^{2}}=\frac{1-i}{2i}=\frac{(1-i)(-i)}{-2{i}^{2}}$=$\frac{-1-i}{2}=-\frac{1}{2}-\frac{1}{2}i$,
∴z在复平面内所对应的点的坐标为($-\frac{1}{2},-\frac{1}{2}$),位于第三象限.
故选:C.
点评 本题考查复数代数形式的乘除运算,考查复数的代数表示法及其几何意义,是基础题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
13.已知复数z满足(1+i)z=2i,则|z|=( )
| A. | $\sqrt{2}$ | B. | $\sqrt{3}$ | C. | 2 | D. | 3 |
14.已知函数f(x)=x2+ax+b(a,b∈R),记集合A={x∈R|f(x)≤0},B={x∈R|f(f(x)+1)≤0},若A=B≠∅,则实数a的取值范围为( )
| A. | [-4,4] | B. | [-2,2] | C. | [-2,0] | D. | [0,4] |
11.设a=log32,b=ln2,c=5-0.5,则( )
| A. | a<b<c | B. | b<c<a | C. | c<a<b | D. | c<b<a |
8.设F为双曲线C:$\frac{x^2}{a^2}-\frac{y^2}{b^2}=1(a>0,b>0)$的右焦点,过坐标原点的直线依次与双曲线C的左、右支交于点P,Q,若|PQ|=2|QF|,∠PQF=60°,则该双曲线的离心率为( )
| A. | $\sqrt{3}$ | B. | $1+\sqrt{3}$ | C. | $2+\sqrt{3}$ | D. | $4+2\sqrt{3}$ |
14.下列函数在区间[0,+∞)上是增函数的是( )
①y=2x ②y=x2+2x-1 ③y=|x+2|④y=|x|+2.
①y=2x ②y=x2+2x-1 ③y=|x+2|④y=|x|+2.
| A. | ①② | B. | ①③ | C. | ②③④ | D. | ①②③④ |
15.执行如图程序框图(见上图),如果输入的x,t均为2,S=( )


| A. | 7 | B. | 6 | C. | 5 | D. | 4 |
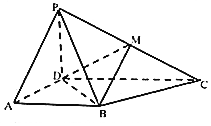 如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点.
如图,四棱锥P-ABCD中,平面PAD⊥平面ABCD,△PAD是正三角形,底面ABCD是直角梯形,AB∥CD,CD⊥AD,CD=2AB=2AD=2,M为PC的中点. 如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.
如图,矩形ABCD中,$AB=2\sqrt{2}$,$AD=\sqrt{2}$,M为DC的中点,将△DAM沿AM折到△D′AM的位置,AD′⊥BM.