题目内容
求过点(2,0)且与曲线y=x3相切的直线方程.
考点:利用导数研究曲线上某点切线方程
专题:计算题,导数的概念及应用
分析:设切点为(m,n),求出导数,求得x=m处的切线的斜率,写出切线方程,代入点(2,0),再由切点满足曲线方程,解m,n的方程,可得m,进而得到切线的斜率,以及切线方程.
解答:
解:设切点为(m,n),
y=x3的导数为y′=3x2,
则切线的斜率为k=3m2,
切线的方程为y-n=3m2(x-m),
代入点(2,0),可得n=3m2(m-2),
又n=m3,
即有m3=3m2(m-2),
解得m=0或3,
即有切线的斜率为0或27.
则过点(2,0)且与曲线相切的切线方程为
y=0或27x-y-54=0.
y=x3的导数为y′=3x2,
则切线的斜率为k=3m2,
切线的方程为y-n=3m2(x-m),
代入点(2,0),可得n=3m2(m-2),
又n=m3,
即有m3=3m2(m-2),
解得m=0或3,
即有切线的斜率为0或27.
则过点(2,0)且与曲线相切的切线方程为
y=0或27x-y-54=0.
点评:本题考查导数的运用:求切线方程,考查直线方程的点斜式,注意在某点处的切线和过某点的切线的区别,设出切点,正确求导是解题的关键.

练习册系列答案
 名题金卷系列答案
名题金卷系列答案
相关题目
设数列{an}为公差为2的等差数列,记{an}的前n项和为Sn,令bn=Sn+an,若{bn}为递增数列,则a1的取值范围是( )
| A、(-4,+∞) |
| B、(-3,+∞) |
| C、(-2,+∞) |
| D、(0,+∞) |
如图所示,程序框图算法流程图的输出结果s的值为( )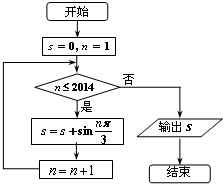

A、
| ||||
B、
| ||||
C、-
| ||||
D、
|
