题目内容
设定义在D上的函数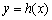 在点
在点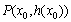 处的切线方程为
处的切线方程为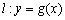 ,当
,当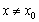 时,若
时,若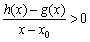 在D内恒成立,则称P为函数
在D内恒成立,则称P为函数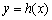 的“类对称点”,则
的“类对称点”,则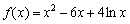 的“类对称点”的横坐标是( )
的“类对称点”的横坐标是( )
A.1 B.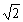 C.
C.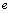 D.
D.
B
解析:由于 ,则在点P处切线的斜率
,则在点P处切线的斜率
 .
.
所以切线方程为

 ,
,
则 ,
, .
.
当 时,
时, 在
在 上单调递减,所以当
上单调递减,所以当 时,
时, 从而有
从而有 时,
时, ;
;
当 时,
时, 在
在 上单调递减,所以当
上单调递减,所以当 时,
时, 从而有
从而有 时,
时, ;
;
所以在 上不存在“类对称点”. 当
上不存在“类对称点”. 当 时,
时, ,所以
,所以 在
在 上是增函数,故
上是增函数,故
所以 是一个类对称点的横坐标. (可以利用二阶导函数为0,求出
是一个类对称点的横坐标. (可以利用二阶导函数为0,求出 ,则
,则 。
。

练习册系列答案
相关题目
 }中,
}中,
 则
则 的最大值为 .
的最大值为 . 中自变量x的取值范围是 .
中自变量x的取值范围是 .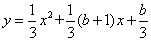 与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.
与x轴交于点A、B(点A位于点B的右侧),与y轴负半轴交于点C,顶点为D.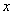 ,
,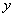 )是
)是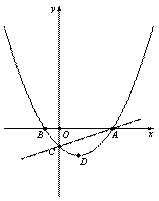
 构成平面区域
构成平面区域 (其中
(其中 ,
, 是变量)。若目标函数
是变量)。若目标函数 的最小值为-6,则实数
的最小值为-6,则实数 的值为( )
的值为( ) B.6 C.3 D.
B.6 C.3 D.
 的解集为
的解集为

 的前四项和
的前四项和 成等比.
成等比. ,若
,若 恒成立,求实数
恒成立,求实数 的最小值.
的最小值.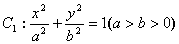 的离心率为
的离心率为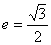 ,且过点
,且过点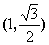 ,抛物线
,抛物线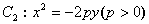 的焦点坐标为
的焦点坐标为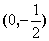 .
.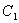 和抛物线
和抛物线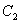 的方程;
的方程;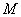 是直线
是直线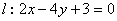 上的动点,过点
上的动点,过点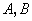 ,直线
,直线 交椭圆
交椭圆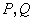 两点.
两点.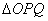 的面积取最大值时,求直线
的面积取最大值时,求直线