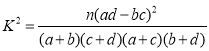题目内容
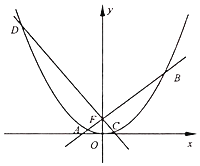
【题目】已知椭圆![]() 的左焦点在抛物线
的左焦点在抛物线![]() 的准线上,且椭圆的短轴长为2,
的准线上,且椭圆的短轴长为2,![]() 分别为椭圆的左,右焦点,
分别为椭圆的左,右焦点,![]() 分别为椭圆的左,右顶点,设点
分别为椭圆的左,右顶点,设点![]() 在第一象限,且
在第一象限,且![]() 轴,连接
轴,连接![]() 交椭圆于点
交椭圆于点![]() ,直线
,直线![]() 的斜率为
的斜率为![]() .
.
(Ⅰ)求椭圆的方程;
(Ⅱ)若三角形![]() 的面积等于四边形
的面积等于四边形![]() 的面积,求
的面积,求![]() 的值;
的值;
(Ⅲ)设点![]() 为
为![]() 的中点,射线
的中点,射线![]() (
(![]() 为原点)与椭圆交于点
为原点)与椭圆交于点![]() ,满足
,满足![]() ,求
,求![]() 的值.
的值.
【答案】(Ⅰ)![]() (Ⅱ)
(Ⅱ)![]() (Ⅲ)
(Ⅲ)![]()
【解析】
(I)根据抛物线的准线求得![]() ,根据短轴长求得
,根据短轴长求得![]() ,由此求得
,由此求得![]() ,进而求得椭圆方程.(II)设出直线
,进而求得椭圆方程.(II)设出直线![]() 的方程,联立直线
的方程,联立直线![]() 的方程和椭圆方程,求得
的方程和椭圆方程,求得![]() 点的坐标,令
点的坐标,令![]() 求得
求得![]() 点坐标.利用三角形的面积公式计算出
点坐标.利用三角形的面积公式计算出![]() 和
和![]() 的面积,根据题目已知条件,这两个三角形的面积相等,由此列方程,解方程求得
的面积,根据题目已知条件,这两个三角形的面积相等,由此列方程,解方程求得![]() 的值.(III)根据(II)求得
的值.(III)根据(II)求得![]() 点坐标,由此求得
点坐标,由此求得![]() 的斜率,设
的斜率,设![]() 所在直线方程为
所在直线方程为![]() ,代入椭圆方程,求得
,代入椭圆方程,求得![]() 点坐标,计算出
点坐标,计算出![]() 到直线
到直线![]() 的距离
的距离![]() ,
,![]() 的长度,化简
的长度,化简![]() 得到
得到![]() ,利用
,利用![]() 列方程,解方程求得
列方程,解方程求得![]() 的值.
的值.
解:(Ⅰ)由已知得,![]() ,故
,故![]() ,椭圆方程为:
,椭圆方程为:![]() ,
,
(Ⅱ)设![]() 直线方程为
直线方程为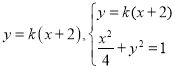 ∴
∴![]()
∴![]() ∴
∴![]()
∴![]() ,令
,令![]() ∴
∴![]()
∴![]()
∴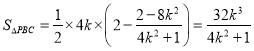
∵![]() ∴
∴![]()
(Ⅲ)由(II)和中点坐标公式,得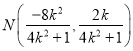 ,设
,设![]() 所在直线方程为
所在直线方程为![]() ,则
,则
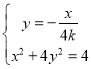 ,∴
,∴![]() ∴
∴ ,
,
![]() 到直线
到直线![]() 的距离:
的距离: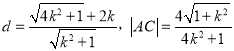 ,
,![]() ,
,
∴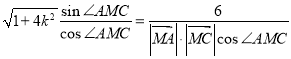
即![]() ,
,
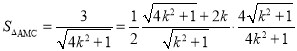 ,化简得
,化简得![]() ,
,
∵![]() ,∴
,∴![]() .
.

 通城学典默写能手系列答案
通城学典默写能手系列答案 金牌教辅培优优选卷期末冲刺100分系列答案
金牌教辅培优优选卷期末冲刺100分系列答案【题目】截至2019年,由新华社《瞭望东方周刊》与瞭望智库共同主办的"中国最具幸福感城市"调查推选活动已连续成功举办12年,累计推选出60余座幸福城市,全国约9亿多人次参与调查,使"城市幸福感"概念深入人心.为了便于对某城市的"城市幸福感"指数进行研究,现从该市抽取若干人进行调查,绘制成如下不完整的2×2列联表(数据单位:人).
男 | 女 | 总计 | |
非常幸福 | 11 | 15 | |
比较幸福 | 9 | ||
总计 | 30 |
(1)将列联表补充完整,并据此判断是否有90%的把握认为城市幸福感指数与性别有关;
(2)若感觉"非常幸福"记2分,"比较幸福"记1分,从上表男性中随机抽取3人,记3人得分之和为![]() ,求
,求![]() 的分布列,并根据分布列求
的分布列,并根据分布列求![]() 的概率
的概率
附: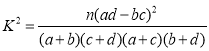 ,其中
,其中![]() .
.
| 0. 10 | 0. 05 | 0. 010 | 0.001 |
| 2.706 | 3.841 | 6. 635 | 10. 828 |