题目内容

4．设集合A={（x1，x2，x3，x4）|xi∈{-1，0，1}，i=1，2，3，4}，那么集合A中满足条件“$x_1^2+x_2^2+x_3^2+x_4^2≤4$”的元素个数为（　　）
A．60B．65C．80D．81

分析 由题意，每个元素都有3种取法，即可得出结论．

解答 解：由题意，每个元素都有3种取法，
∴元素个数为34=81．
故选D．

点评 本题看似集合题，其实考察的是用排列组合思想去解决问题．

练习册系列答案
相关题目
14．已知不等式ax2-3x+2＞0
（1）若a=-2，求上述不等式的解集；
（2）若上述不等式的解集为{x|x＜1或x＞b}，求a，b的值．
15．集合A={x|x2-a≤0}，B={x|x＜2}，若A⊆B，则实数a的取值范围是（　　）
A．（-∞，4]B．（-∞，4）C．[0，4]D．（0，4）
12．空间直角坐标系中，下列点在x 轴上的是（　　）
A．（0.1，0.2，0.3）B．（0，0，0.001）C．（5，0，0）D．（0，0.01，0）
19．i为虚数单位，已知复数z满足$\frac{2}{1+i}=\overline z+i$，则z=（　　）
A．1+iB．-1+iC．1+2iD．1-2i
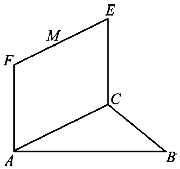9．如图，矩形ACEF和等边三角形ABC中，AC=2，CE=1，平面ABC⊥平面ACEF．
（1）在EF上找一点M，使BM⊥AC，并说明理由；
（2）在（1）的条件下，求平面ABM与平面CBE所成锐二面角余弦值．
16．已知函数f（x）=xlnx+2，g（x）=x2-mx．
（1）求函数f（x）在[t，t+2]（t＞0）上的最小值；
（2）若存在x0∈[$\frac{1}{e}$，e]使得mf′（x0）+g（x0）≥2x0+m成立，求实数m的取值范围．
13．等比数列{an}中，a1=1，a8=4，函数f（x）=x（x-a1）（x-a2）（x-a3）…（x-an），若y=f（x）的导函数为y=f'（x），则f'（0）=（　　）
A．1B．28C．212D．215
14．执行如图程序语句，输入a=2cos$\frac{2017π}{3}$，b=2tan$\frac{2017π}{4}$，则输出y的值是（　　）
A．3B．4C．6D．-1

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网