题目内容
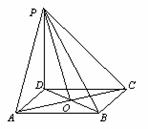
已知边长为6的正方形ABCD所在平面外一点P,PD^平面ABCD,PD=8,
(1)连接PB、AC,证明:PB ^ AC;
(2)求PB与平面ABCD所成的角的大小;
(3)求点D到平面PAC的距离.
|
(1)证明:连接BD,交AC于O,在正方形ABCD中,AC ^ BD,
又PD^平面ABCD,所以,PD^AC,……………………………………2分
所以AC ^平面PBD,故PB ^ A C.……………………………………4分
|
在DPBD中,PD=8,BD=6![]()
所以 tanÐPBD = ![]()
ÐAPO=arctan![]() …………………………8分
…………………………8分
PB与平面ABCD所成的角的大小为arctan![]() ……………………………………9分
……………………………………9分
(3)解:连接PC,设点D到平面PAC的距离为h,……………………………10分
则有VD–PAC =VP–ACD,即:![]() ´ SDPAC ´ h =
´ SDPAC ´ h =![]() ´PD´AD´DC………………………12分
´PD´AD´DC………………………12分
在DPAC中,连结PO,显然PO^AC,PO=![]()
h = ![]()
所以点D到平面PAC的距离为![]() ……………………………………14分
……………………………………14分

练习册系列答案
 暑假衔接培优教材浙江工商大学出版社系列答案
暑假衔接培优教材浙江工商大学出版社系列答案 欣语文化快乐暑假沈阳出版社系列答案
欣语文化快乐暑假沈阳出版社系列答案
相关题目
 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 2 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
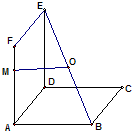 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 3 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
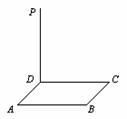
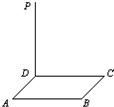 已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,
已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8, 如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小
如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小 (2008•上海模拟)已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,
(2008•上海模拟)已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,