题目内容
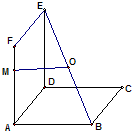
 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 2 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
分析:过O作OH垂直底面于H,则H一定在对角线AC上,且是其中点,AC的长度是6
,可证得线段OM与线段AH等长,而AH的长度是AC长度的一半,所以线段OM的长度为3
.
| 2 |
| 2 |
解答: 解:如图,过O作OH⊥面ABCD于H,
解:如图,过O作OH⊥面ABCD于H,
∵边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
∴H点在AC的中点上且OH
AM,
∴四边形AMOH是平行四边形
∴OM=AH
又AC=2AH=6
∴OM=AH=3
.
故应选A.
 解:如图,过O作OH⊥面ABCD于H,
解:如图,过O作OH⊥面ABCD于H,∵边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
∴H点在AC的中点上且OH
| ||
. |
∴四边形AMOH是平行四边形
∴OM=AH
又AC=2AH=6
| 2 |
∴OM=AH=3
| 2 |
故应选A.
点评:考查面面垂直的性质,本题主要训练答题者的空间立体感,培养答题者的空间想象能力.

练习册系列答案
相关题目
 已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,
已知边长为6的正方形ABCD和正方形ADEF所在平面互相垂直,O是BE中点,| FM |
| 1 |
| 3 |
| FA |
A、3
| ||
B、
| ||
C、2
| ||
D、
|
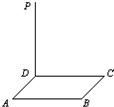 已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,
已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8, 如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小
如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小 (2008•上海模拟)已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,
(2008•上海模拟)已知边长为6的正方形ABCD所在平面外一点P,PD⊥平面ABCD,PD=8,