题目内容
 如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小
如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小arcsin
3
| ||
| 10 |
arcsin
(用反三角函数表示)3
| ||
| 10 |
分析:连接AC、BD,相交与点O,连接PO,根据线面垂直的判定定理可证AC⊥面PDB,则∠APO为PA与平面PBD所成角,然后在直角三角形APO中求出此角的正弦值即可.
解答:解: 连接AC、BD,相交与点O,连接PO
连接AC、BD,相交与点O,连接PO
∵正方形ABCD
∴AC⊥BD
而PD⊥平面ABCD,AC?平面ABCD
∴AC⊥PD而PD∩BD=D
∴AC⊥面PDB
∴∠APO为PA与平面PBD所成角
AO=3
,PA=10
∴sin∠APO=
∴PA与平面PBD所成角的大小为arcsin
故答案为:arcsin
 连接AC、BD,相交与点O,连接PO
连接AC、BD,相交与点O,连接PO∵正方形ABCD
∴AC⊥BD
而PD⊥平面ABCD,AC?平面ABCD
∴AC⊥PD而PD∩BD=D
∴AC⊥面PDB
∴∠APO为PA与平面PBD所成角
AO=3
| 2 |
∴sin∠APO=
3
| ||
| 10 |
∴PA与平面PBD所成角的大小为arcsin
3
| ||
| 10 |
故答案为:arcsin
3
| ||
| 10 |
点评:本题主要考查了线面所成角的度量,解题的关键就是寻找线面所成角,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
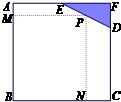 (2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为
(2013•杨浦区一模)如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.则矩形BNPM面积的最大值为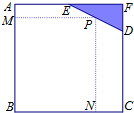 如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值.
如图,已知边长为8米的正方形钢板有一个角锈蚀,其中AE=4米,CD=6米.为了合理利用这块钢板,将在五边形ABCDE内截取一个矩形块BNPM,使点P在边DE上.求矩形BNPM面积的最大值. 如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小________(用反三角函数表示)
如图,已知边长为6的正方形ABCD所在平面外的一点P,PD⊥平面ABCD,PD=8,连接PA,则PA与平面PBD所 成角的大小________(用反三角函数表示)