题目内容
把半径为1的四个小球垒成两层放在桌子上,下层放3个,上层放1个,两两相切,求上层的最高点离桌面的距离.
考点:球的体积和表面积
专题:计算题,空间位置关系与距离
分析:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且各棱长均为2R,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高,由此可求上面一个球的球心到桌面的距离.
解答:
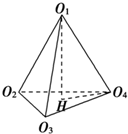 解:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且各棱长均为4,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.
解:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且各棱长均为4,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.
连接O4H,则O4H=
,
∵O1H⊥面O2O3O4,
∴O1H⊥HO4,即∠O1HO4=90°,∴O1H=
,
则从上面一个球的球心到桌面的距离为
+1.
上层的最高点离桌面的距离:
+1.
 解:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且各棱长均为4,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.
解:设四个球的球心分别为O1、O2、O3、O4,将它们两两连结恰好组成一个正三棱锥,且各棱长均为4,作O1H⊥面O2O3O4,垂足为H,则O1H为棱锥的高.连接O4H,则O4H=
2
| ||
| 3 |
∵O1H⊥面O2O3O4,
∴O1H⊥HO4,即∠O1HO4=90°,∴O1H=
2
| ||
| 3 |
则从上面一个球的球心到桌面的距离为
2
| ||
| 3 |
上层的最高点离桌面的距离:
2
| ||
| 3 |
点评:本题考查点到面的距离的计算,考查学生分析解决问题的能力,考查学生转化问题的能力,属于中档题.

练习册系列答案
相关题目
椭圆的长轴为2,离心率为
,则其短半轴为( )
| 1 |
| 2 |
A、
| ||||
B、
| ||||
C、
| ||||
D、
|
已知等差数列{an}单调递增,且满足a1,a10是方程x2-4x+a=0的两根,则a8的取值范围是( )
| A、(2,4) |
| B、(-∞,2) |
| C、(2,+∞) |
| D、(4,+∞) |
如图是求函数值的算法流程图,当输入值为2时,则输出值为( )


| A、4 | B、0 | C、1 | D、-3 |
已知函数y=Asin(ωx+φ)(A>0,ω>0,|φ|<
)的图象如图所示,则其表达式为( )
| π |
| 2 |

A、y=3sin(2x+
| ||
B、y=3sin(4x+
| ||
C、y=3sin(2x-
| ||
D、y=3sin(4x-
|