Question

【题目】【2018山西太原市高三3月模拟】已知椭圆的左、右顶点分别为，右焦点为，点在椭圆上．

（I）求椭圆方程；

（II）若直线与椭圆交于两点，已知直线与相交于点，证明：点在定直线上，并求出定直线的方程．

Answer 1

【答案】（I）；（II）定直线．

【解析】试题分析：(1)将点坐标代入椭圆方程，解方程组可得 (2)先根据特殊位置计算交点在定直线上，再设，解方程组可得交点横坐标，联立直线方程与椭圆方程，利用韦达定理代入化简可得定值1.

试题解析：

（1），∴ ，由题目已知条件知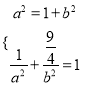，∴ ，所以；

（2）由椭圆对称性知在上，假设直线过椭圆上顶点，则，

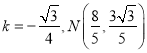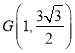∴， ，∴ ，所以在定直线上．

当不在椭圆顶点时，设， 得，

所以，

，当时， 得，

所以显然成立，所以在定直线上．