题目内容
(本小题满分12分)已知函数
 .
.
(1)求 的单调递增区间;
的单调递增区间;
(2)在锐角三角形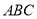 中,a、b、c分别是角A、B、C的对边,若
中,a、b、c分别是角A、B、C的对边,若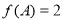 ,
, ,
, 的面积为
的面积为 ,求
,求 的值.
的值.
(1)
由 ,得
,得 ,
,
所求 的单调递增区间为
的单调递增区间为 ,
, 6分
6分
(2)在锐角三角形 中,
中, ,得
,得 ,
,
由 ,则
,则 ,所以
,所以 ,解得
,解得 .
.
又因为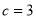 ,
, 的面积为
的面积为
所以 ,解得
,解得 .
.
所求 12分
12分
【解析】
试题分析(1)化简函数的解析式为f(x)=2sin(2x﹣ ),令2kπ﹣
),令2kπ﹣ ≤2x﹣
≤2x﹣ ≤2kπ+
≤2kπ+ ,k∈z,求得x的范围,可得函数的增区间.
,k∈z,求得x的范围,可得函数的增区间.
(2)根据 f(A)=2=2sin(2A﹣ )=2,求得A的值,再由S△ABC=
)=2,求得A的值,再由S△ABC= bc•sinA=3
bc•sinA=3 解得b的值,从而利用余弦定理得a的值.
解得b的值,从而利用余弦定理得a的值.
考点:两角和差公式,三角函数的图像与性质,正弦定理.

练习册系列答案
相关题目
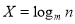 ,则
,则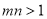 是
是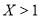 的( )。
的( )。 =
= .将函数
.将函数 的图象向左平移
的图象向左平移 个单位,以下是所得函数图象的一个对称中心是( )
个单位,以下是所得函数图象的一个对称中心是( ) B.
B. C.
C. D.
D.
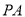 与圆
与圆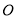 相切于点
相切于点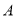 ,经过点
,经过点 的割线
的割线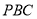 交圆
交圆 于点
于点 和点
和点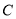 ,
,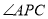 的平分线分别交AB、AC于点
的平分线分别交AB、AC于点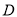 和
和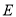 .
.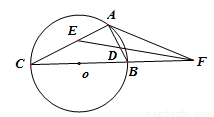
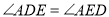 ;
;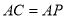 ,求
,求 的值.
的值. 是定义在
是定义在 上的增函数,函数
上的增函数,函数 的图像关于点
的图像关于点 对称,
对称, 、
、 ,不等式
,不等式 恒成立,则当
恒成立,则当 时,
时, 的
的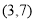 B.
B. C.
C. D.
D.
 的前
的前 项和为
项和为 ,若
,若 ,
, ,则
,则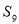 等于
等于 B.
B. C.
C. D.
D.
 ,
, ,则使不等式
,则使不等式 成立的最大自然数
成立的最大自然数 为____________
为____________ 的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( )
的球面上,过P作两两垂直的三条弦,若其中一条弦长是另一条弦长的2倍,则这三条弦长之和的最大值是( ) D.
D.