题目内容
16. 如图,已知Rt△OAB中,∠AOB=90°,OA=3,OB=2,M在OB上,且OM=1,N在OA上,且ON=1,P为AM与BN的交点,求∠MPN.(要求用向量求解).
如图,已知Rt△OAB中,∠AOB=90°,OA=3,OB=2,M在OB上,且OM=1,N在OA上,且ON=1,P为AM与BN的交点,求∠MPN.(要求用向量求解).
分析 用$\overrightarrow{OA},\overrightarrow{OB}$表示出$\overrightarrow{AM},\overrightarrow{BN}$,求出$\overrightarrow{AM},\overrightarrow{BN}$的夹角即为∠MPN.
解答 解:∵OA=3,OB=2,OM=ON=1,则$\overrightarrow{OM}$=$\frac{1}{2}$$\overrightarrow{OB}$,$\overrightarrow{ON}$=$\frac{1}{3}$$\overrightarrow{OA}$,
∴|$\overrightarrow{AM}$|=$\sqrt{O{A}^{2}+O{M}^{2}}$=$\sqrt{10}$,|$\overrightarrow{BN}$|=$\sqrt{O{B}^{2}+O{N}^{2}}$=$\sqrt{5}$.
又∵$\overrightarrow{AM}$=$\overrightarrow{OM}$-$\overrightarrow{OA}$=$\frac{1}{2}$$\overrightarrow{OB}$-$\overrightarrow{OA}$,$\overrightarrow{BN}$=$\overrightarrow{ON}$-$\overrightarrow{OB}$=$\frac{1}{3}$$\overrightarrow{OA}$-$\overrightarrow{OB}$,
∵∠AOB=90°,∴$\overrightarrow{OA}•\overrightarrow{OB}=0$.
∴$\overrightarrow{AM}$•$\overrightarrow{BN}$=($\frac{1}{2}$$\overrightarrow{OB}$-$\overrightarrow{OA}$)•($\frac{1}{3}$$\overrightarrow{OA}$-$\overrightarrow{OB}$)=-$\frac{1}{2}{\overrightarrow{OB}}^{2}-\frac{1}{3}{\overrightarrow{OA}}^{2}$=-5,
设$\overrightarrow{AM}$,$\overrightarrow{BN}$的夹角为θ,
∴cosθ=$\frac{-5}{\sqrt{5}•\sqrt{10}}$=-$\frac{\sqrt{2}}{2}$,
又∵θ∈[0,π],∴θ=$\frac{3π}{4}$,
又∵∠MPN即为向量$\overrightarrow{AM}$,$\overrightarrow{BN}$的夹角,
∴∠MPN=$\frac{3π}{4}$.
点评 问题考查了平面向量在几何中的应用,属于基础题.

 新思维寒假作业系列答案
新思维寒假作业系列答案| A. | {x|x≥-4} | B. | {x|x>-4} | C. | {x|x≥-2} | D. | {x|x>-2} |
| A. | 1 | B. | -1 | C. | 0 | D. | -2 |
| A. | f′(a)>0 | B. | f′(a)<0 | C. | f′(a)=0 | D. | f'(a)不存在 |
| A. | p∧q | B. | p∧(¬q) | C. | (¬p)∧q | D. | (¬p)∧(¬q) |
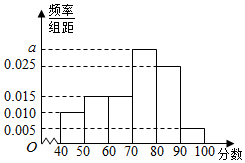 某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).
某校从参加环保知识竞赛的学生中抽出60名,将其成绩(均为整数)分成六段[40,50),[50,60),…,[90,100]后得到频率分布直方图(如图所示).