题目内容
已知复数z满足（2+i）（1-i）=i•z（i为虚数单位），则z=（ ）A．-1+3i
B．-1-3i
C．1+3i
D．1-3i
【答案】分析：由条件可得 z=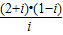
=
=（3-i）（-i），化简可得结果．
解答：解：∵复数z满足（2+i）（1-i）=i•z，∴z=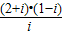
=
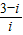=（3-i）（-i）=-1-3i，
故选 B．
点评：本题考查两个复数代数形式的乘除法，两个复数相除，分子和分母同时乘以分母的共轭复数．
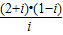==（3-i）（-i），化简可得结果．解答：解：∵复数z满足（2+i）（1-i）=i•z，∴z=
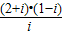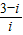==（3-i）（-i）=-1-3i，故选 B．
点评：本题考查两个复数代数形式的乘除法，两个复数相除，分子和分母同时乘以分母的共轭复数．
练习册系列答案
阅读快车系列答案
相关题目
已知复数z满足（2+i）（1-i）=i•z（i为虚数单位），则z=（ ）
| A、-1+3i | B、-1-3i | C、1+3i | D、1-3i |
已知复数z满足（2-i）z=5（i为虚数单位）则|z|=（ ）
A、
| ||
| B、3 | ||
| C、2 | ||
| D、1 |