题目内容
11．求焦点是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点的抛物线的标准方程．分析 求出题意的左焦点坐标，得到抛物线的焦点坐标，然后然后求解抛物线的标准方程．
解答 解：椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点（-1，0），
焦点是椭圆$\frac{{x}^{2}}{4}$+$\frac{{y}^{2}}{3}$=1的左焦点的抛物线，可得p=2，
抛物线的标准方程为：y2=-4x．
点评 本题考查题意的简单性质以及抛物线的标准方程的求法，考查计算能力．
练习册系列答案
相关题目
1．下列命题正确的是（ ）
| A． | 若两条直线和同一个平面所成的角相等，则这两条直线平行 | |
| B． | 若一个平面内有三个点到另一个平面的距离相等，则这两个平面平行 | |
| C． | 三角形的两条边平行于一个平面，则第三边也平行于这个平面 | |
| D． | 若两个平面都垂直于第三个平面，则这两个平面平行 |
2．不等式|3x+6|≤21的解集是（ ）
| A． | ∅ | B． | [-9，5] | C． | （-∞，-9）∪（5，+∞） | D． | R |
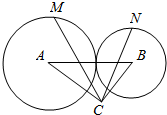如图，圆A与圆B外切，半径分别为3，2，且△ABC是以C为直角顶点的Rt△．若AC=4．BC=3，点M，N分别在圆A，B上，则$\overrightarrow{CM}$•$\overrightarrow{CN}$的取值范围是[-6-$\sqrt{145}$，6+$\sqrt{145}$]．
20．函数y=2${\;}^{-{x}^{2}-3x+2}$的单调递增区间为（ ）
| A． | （-$∞，\frac{3}{2}$） | B． | （$\frac{3}{2}，+∞$） | C． | （-$∞，-\frac{3}{2}$） | D． | （-$\frac{3}{2}，+∞$） |
5．“ab=0”是“a=0”的（ ）条件．
| A． | 必要不充分 | B． | 充分不必要 | ||
| C． | 充要 | D． | 既不充分也不必要 |