题目内容
15.已知A,B为圆x2+(y-1)2=4上关于点P(1,2)对称的两点,则直线AB的方程为( )| A. | x+y-3=0 | B. | x-y+3=0 | C. | x+3y-7=0 | D. | 3x-y-1=0 |
分析 求出圆心坐标,利用圆x2+(y-1)2=4上存在A,B两点关于点P(1,2)成中心对称,求出直线AB的斜率,进而可求直线AB的方程.
解答 解:由题意,圆x2+(y-1)2=4的圆心坐标为C(0,1),
∵圆x2+(y-1)2=4上存在A,B两点关于点P(1,2)成中心对称,
∴CP⊥AB,P为AB的中点,
∵kCP=$\frac{2-1}{1-0}$=1,∴kAB=-1,
∴直线AB的方程为y-2=-(x-1),即x+y-3=0.
故选:A.
点评 本题考查直线与圆的位置关系,考查圆的对称性,考查学生的计算能力,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目
3.某工厂共有甲、乙、丙三个车间,甲车间有x名职工,乙车间有300名职工,丙车间有y名职工,现采用分层抽样的方法从该厂抽取容量为45人的样本,甲车间抽取20人,丙车间抽取10人,则该工厂共有的职工人数是( )
| A. | 600人 | B. | 800人 | C. | 900人 | D. | 1000人 |
10.在六条棱长均相等的三棱锥A-BCD中,已知M,N,K分别是棱AB,CD,AC的中点,则下列结论中:
①MN∥AD;②NK∥平面ABD;③AB⊥CD;④平面CDM⊥平面ABN,正确的个数有( )
①MN∥AD;②NK∥平面ABD;③AB⊥CD;④平面CDM⊥平面ABN,正确的个数有( )
| A. | 1个 | B. | 2个 | C. | 3个 | D. | 4个 |
20.下列函数:①y=-$\frac{1}{x+1}$;②y=(x-1)3;y=log2x-1;④y=-($\frac{1}{2}$)|x|中,在(0,+∞)上是增函数且不存在零点的函数的序号是( )
| A. | ①④ | B. | ②③ | C. | ②④ | D. | ①③④ |
7.已知tanα<0,|cosα|=cosα,则α是( )
| A. | 第一象限角 | B. | 第二象限角 | C. | 第三象限角 | D. | 第四象限角 |
4.执行如图所示的程序框图,如果输入的N=2016,那么输出的S=( )
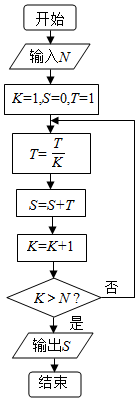

| A. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2015}$ | B. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2015!}$ | ||
| C. | 1+$\frac{1}{2}$+$\frac{1}{3}$+…+$\frac{1}{2016}$ | D. | 1+$\frac{1}{2!}$+$\frac{1}{3!}$+…+$\frac{1}{2016!}$ |