题目内容
18.已知$f(x)=\frac{x}{1+x},x≥0$,若f1(x)=f(x),fn+1(x)=f(fn(x)),n∈N+,归纳猜想f2018(x)的表达式为f2018(x)=$\frac{x}{1+2018x}$.分析 由题意,可先求出f1(x),f2(x),f3(x)…,归纳出fn(x)的表达式,即可得出f2018(x)的表达式
解答 解:由题意f1(x)=$f(x)=\frac{x}{1+x},x≥0$,
f2(x)=f(f1(x))=$\frac{\frac{x}{1+x}}{1+\frac{x}{1+x}}$=$\frac{x}{1+2x}$,
…
fn(x)=f(fn-1(x))=$\frac{x}{1+nx}$,
∴f2018(x)=$\frac{x}{1+2018x}$,
故答案为:f2018(x)=$\frac{x}{1+2018x}$.
点评 本题考查逻辑推理中归纳推理,由特殊到一般进行归纳得出结论是此类推理方法的重要特征.

练习册系列答案
 挑战100单元检测试卷系列答案
挑战100单元检测试卷系列答案
相关题目
9.在△ABC中,内角A,B,C所对应的边分别为a,b,c,且asin2B+bsinA=0,若△ABC的面积S=$\sqrt{3}$b,则△ABC面积的最小值为( )
| A. | 1 | B. | 12$\sqrt{3}$ | C. | 8$\sqrt{3}$ | D. | 12 |
6.已知函数$y=\frac{1}{3}{x^3}+b{x^2}+(b+2)x+3$在R上单调递增,则b的取值范围为( )
| A. | [0,1] | B. | [1,2] | C. | [-1,2] | D. | [1,+∞] |
3.以下关于正弦定理或其变形的叙述错误的是( )
| A. | 在△ABC中,a:b:c=sinA:sinB:sinC | |
| B. | 在△ABC中,若sin2A=sin2B,则a=b | |
| C. | 在△ABC中,若sinA>sinB,则A>B,若A>B,则sinA>sinB | |
| D. | 在△ABC中,$\frac{a}{sinA}=\frac{b+c}{sinB+sinC}$ |
10.设α=-300°,则与α终边相同的角的集合为( )
| A. | {α|α=k•360°+300°,k∈Z} | B. | {α|α=k•360°+60°,k∈Z} | ||
| C. | {α|α=k•360°+30°,k∈Z} | D. | {α|α=k•360°-60°,k∈Z} |
7.下列函数中,周期为$\frac{π}{2}$的偶函数为( )
| A. | y=sin4x | B. | y=cos2x | C. | y=tan2x | D. | $y=sin(\frac{π}{2}-4x)$ |
8.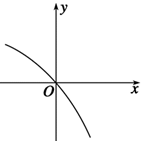 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )| A. | (1,6) | B. | (-1,5) | C. | (0,5) | D. | (3,+∞) |