题目内容
8.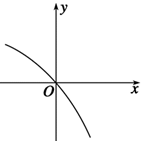 已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )
已知函数f(x)的定义域为R,f′(x)为f(x)的导函数,函数y=f′(x)的图象如图所示,且f(-2)=1,f(3)=1,则不等式f(x-3)>1的解集为( )| A. | (1,6) | B. | (-1,5) | C. | (0,5) | D. | (3,+∞) |
分析 判断f(x)的单调性,根据单调性列不等式解出x的范围.
解答 解:由图象可知当x<0时,f′(x)>0,当x>0时,f′(x)<0,当x=0时,f′(x)=0,
∴f(x)在(-∞,0)上单调递增,在(0,+∞)上单调递减,
∴当x=0时,f(x)取得最大值.
∵f(x-3)>1,f(-2)=f(3)=1,
∴-2<x-3<3,
∴1<x<6.
故选A.
点评 本题考查了导数与函数的单调性的关系,函数单调性的应用,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
20.若等差数列{an}的前7项和S7=77,则a4等于( )
| A. | 11 | B. | 12 | C. | 7 | D. | 不能确定 |