题目内容
若实数x,y满足的约束条件
,将一颗骰子投掷两次得到的点数分别为a,b,则函数z=2ax+by在点(2,-1)处取得最大值的概率为( )
|
A、
| ||
B、
| ||
C、
| ||
D、
|
考点:几何概型,简单线性规划
专题:应用题,概率与统计
分析:利用古典概型概率计算公式,先计算总的基本事件数N,再计算事件函数z=2ax+by在点(2,-1)处取得最大值时包含的基本事件数n,最后即可求出事件发生的概率.
解答:
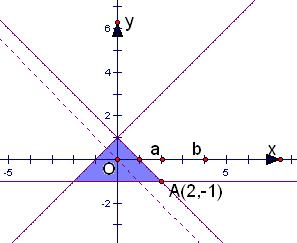 解:画出不等式组
解:画出不等式组
表示的平面区域,
∵函数z=2ax+by在点(2,-1)处取得最大值,
∴直线z=2ax+by的斜率k=-
≤-1,即2a≥b.
∵一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中2a≥b的有(1,1),(1,2),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)共30个
则函数z=2ax+by在点(2,-1)处取得最大值的概率为
=
.
故选:D.
 解:画出不等式组
解:画出不等式组
|
∵函数z=2ax+by在点(2,-1)处取得最大值,
∴直线z=2ax+by的斜率k=-
| 2a |
| b |
∵一颗骰子投掷两次分别得到点数为(a,b),则这样的有序整数对共有6×6=36个
其中2a≥b的有(1,1),(1,2),(2,1),(2,2),(2,3),(2,4),(3,1),(3,2),(3,3),(3,4),(3,5),(3,6),(4,1),(4,2),(4,3),(4,4),(4,5),(4,6)共30个
则函数z=2ax+by在点(2,-1)处取得最大值的概率为
| 30 |
| 36 |
| 5 |
| 6 |
故选:D.
点评:本题考查了古典概型概率的计算方法,乘法计数原理,分类计数原理,属于基础题

练习册系列答案
 每日10分钟口算心算速算天天练系列答案
每日10分钟口算心算速算天天练系列答案
相关题目
设等差数列{an}的公差为d,且a3=2,若数列{2 a1an}为递增数列,则公差d的取值范围是( )
| A、d<0 | B、d>1 |
| C、d>1或d<0 | D、0<d<1 |
已知两个单位向量
,
的夹角为60°,
=(1-t)
+t
,若
•
=-
,则实数t的取值是( )
| a |
| b |
| c |
| a |
| b |
| b |
| c |
| 1 |
| 2 |
| A、2 | ||
| B、-2 | ||
C、
| ||
D、-
|


