题目内容
某隧道入口竖立着“限高4.5米”的警示牌，是指示司机要想安全通过隧道，应使车载货物高度h满足关系为（ ）
| A、h＜4.5 |
| B、h＞4.5 |
| C、h≤4.5 |
| D、h≥4.5 |
考点：不等关系与不等式
专题：不等式的解法及应用
分析：理解“限高”的含义是“≤”即可得出．
解答：
解：“限高4.5米”的意义为“h≤4.5”，
故选：C．
故选：C．
点评：本题考查了理解“限高”的含义是“≤”，属于基础题．
练习册系列答案
习题精选系列答案
相关题目
“x2-4x+3＞0”是“x＜1或x＞4”的（ ）
| A、充分不必要条件 |
| B、必要不充分条件 |
| C、充要条件 |
| D、既不充分也不必要条件 |
已知a、b、c满足a＞b＞c，且a+b+c=0，那么下列选项中不一定成立的是（ ）
| A、ab＞ac |
| B、c（b-a）＜0 |
| C、cb2＜ab2 |
| D、ac（a-c）＜0 |
如图程序运行后输出的结果为（ ）
| A、22；-22 |
| B、-22；22 |
| C、6；-6 |
| D、-6；6 |
设函数f（x）=
的定义域为集合A，集合B={x|x-a+1＜0}，若A∩B≠∅，则a的取值范围是（ ）
| x-2 |
| A、a＞3 | B、a≥3 |
| C、a＜3 | D、a≤3 |
若变量x，y满足条件
，则z=x+y的取值范围是（ ）
|
| A、（-∞，3] |
| B、[3，+∞） |
| C、[0，3] |
| D、[1，3] |
已知函数y=f（x）是定义在（-1，1）上的函数，且对于任意x1，x2∈（-1，1）且x1≠x2，都有
＜0，则关于a的不等式f（1-a）＜f（a2-1）的取值范围是（ ）
| f(x1)-f(x2) |
| x 1-x2 |
| A、-2＜a＜1 | ||
| B、a＞1或a＜-2 | ||
C、0＜a＜
| ||
| D、0＜a＜1 |
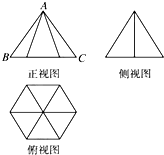一个几何体的三视图如图所示，其中正视图中△ABC是边长为2的正三角形，俯视图为正六边形，求该几何体的侧视图的面积．