题目内容
3．定义min{a，b}=$\left\{\begin{array}{l}{a，a≤b}\\{b，a＞b}\end{array}\right.$，设f（x）=min{x2，$\frac{1}{x}$}，则由函数f（x）的图象与x轴、直线x=2所围成的封闭图形的面积为（ ）| A． | $\frac{7}{12}$ | B． | $\frac{5}{12}$ | C． | $\frac{1}{3}+ln2$ | D． | $\frac{1}{6}+ln2$ |
分析 根据题目给出的函数定义，写出分段函数f（x）=min{x2，$\frac{1}{x}$}，由图象直观看出所求面积的区域，然后直接运用定积分求解阴影部分的面积．
解答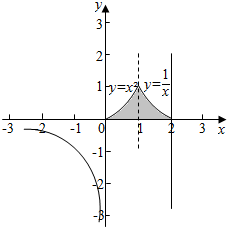 
解：由$\frac{1}{x}$=x2，得：x=1，
又当x＜0时，$\frac{1}{x}$＜x2，
所以，根据新定义有f（x）=min{x2，$\frac{1}{x}$}=$\left\{\begin{array}{l}{{x}^{2}，0＜x≤1}\\{\frac{1}{x}，x＜0或x＞1}\end{array}\right.$，
图象如图，
所以，由函数f（x）的图象与x轴、x=2直线所围成的封闭图形为图中阴影部分，
其面积为S=${∫}_{0}^{1}$x2dx+${∫}_{1}^{2}$$\frac{1}{x}$dx=$\frac{1}{3}{x}^{3}$|${\;}_{0}^{1}$+lnx|${\;}_{1}^{2}$=$\frac{1}{3}$+ln2，
故选：C．
点评 本题考查了定积分在求面积中的应用，考查了新定义，训练了学生的作图能力，解答要用数形结合画出所求面积的区域，此题是中档题．
练习册系列答案
相关题目
13．设集合M={x||x-1|≤1}，N={x|y=lg（x2-1）}，则M∩∁RN=（ ）
| A． | [1，2] | B． | [0，1] | C． | （-1，0） | D． | （0，2） |
11．
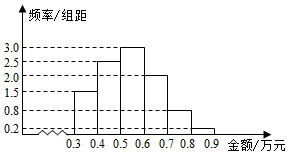某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），
[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
（I）求这1000名购物者获得优惠券金额的平均数；
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．
某电子商务公司随机抽取l000名网络购物者进行调查，这1000名购物者2015年网上购物金额（单位：万元）均在区间[0.3，0.9]内，样本分组为：[0.3，0.4），[0.4，0.5），[0.5，0.6），[0.6，0.7），[0.7，0.8），[0.8，0.9]，购物金额的频率分布直方图如下：电子商务公司决定给购物者发放优惠券，其金额（单位：元）与购物金额关系如下：
| 购物金额分组 | [0.3，0.5） | [0.5，0.6） | [0.6，0.8） | [0.8，0.9] |
| 发放金额 | 50 | 100 | 150 | 200 |
（Ⅱ）以这1000名购物者购物金额落在相应区间的频率作为概率，求一个购物者获得优惠券金额不少于150元的概率．