题目内容
在三棱柱ABC-A1B1C1中，侧面A1ACC1是垂直于底面的菱形，BC⊥A1C1，则A1B与AC1所成的角等于 ．
考点：异面直线及其所成的角
专题：空间位置关系与距离
分析：利用菱形的性质得到AC1⊥A1C，再由侧面A1ACC1是垂直于底面的菱形，BC⊥A1C1，得到AC1⊥面A1BC，利用线面垂直的性质得到所求．
解答：
解：如图，连接A1C，因四边形A1ACC1是菱形，所以AC1⊥A1C
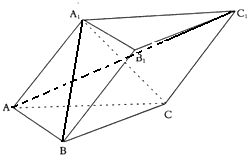
由已知BC⊥A1C1且A1C1∥AC，所以BC⊥AC，
因为侧面A1ACC1是垂直于底面的菱形，所以BC⊥平面A1ACC1，
所以BC⊥AC1，
所以AC1⊥面A1BC
所以AC1⊥A1B；
故答案为：90°．
由已知BC⊥A1C1且A1C1∥AC，所以BC⊥AC，
因为侧面A1ACC1是垂直于底面的菱形，所以BC⊥平面A1ACC1，
所以BC⊥AC1，
所以AC1⊥面A1BC
所以AC1⊥A1B；
故答案为：90°．
点评：本题考查了三棱柱的性质的运用以及线面初中的判定定理和慢慢成长中的性质的运用，体现了转化的思想．
练习册系列答案
天天向上一本好卷系列答案
小学生10分钟应用题系列答案
相关题目
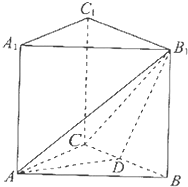如图，在棱长均相等的正三棱柱ABC-A1B1C1中，D为BC的中点．
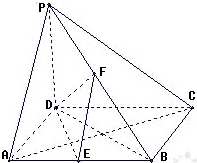已知四棱锥P-ABCD，底面是边长为a的正方形，PD⊥底面ABCD，PD=DC，E、F分别是AB、PB的中点，