题目内容
11.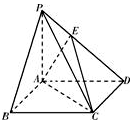 四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$
四棱锥P-ABCD中,底面ABCD是正方形,PB⊥BC,PD⊥CD,E点满足$PE=\frac{1}{3}PD$(1)求证:PA⊥平面ABCD;
(2)在线段BC上是否存在点F使得PF∥面EAC?若存在,确定F的位置;若不存在,请说明理由.
分析 (1)证明BC⊥PA,CD⊥PA,即可证明:PA⊥平面ABCD;
(2)当F为BC中点时,PF∥面EAC,证明PF∥ES即可.
解答 (1)证明:在正方形ABCD中,AB⊥BC
又∵PB⊥BC,AB∩PB=B,
∴BC⊥面PAB,∴BC⊥PA
同理CD⊥PA,
∵BC∩CD=C,∴PA⊥面ABCD
(2)解:当F为BC中点时,PF∥面EAC,理由如下:
∵AD∥2FC,∴$\frac{FS}{SD}=\frac{FC}{AD}=\frac{1}{2}$,
又由已知有$\frac{PE}{ED}$=$\frac{1}{2}$,∴PF∥ES
∵PF?面EAC,EC?面EAC,
∴PF∥面EAC.
点评 本题考查线面平行、线面垂直的证明,考查学生分析解决问题的能力,属于中档题.

练习册系列答案
相关题目
6.下列命题正确的是( )
| A. | 四条线段顺次首尾连接,所得的图形一定是平面图形 | |
| B. | 一条直线和两条平行直线都相交,则三条直线共面 | |
| C. | 两两平行的三条直线一定确定三个平面 | |
| D. | 和两条异面直线都相交的直线一定是异面直线 |
16.已知正项数列{an}中,a1=1,a2=$\sqrt{3},2{a_n}^2={a_{n+1}}^2+{a_{n-1}}$2(n≥2),则a5=( )
| A. | 9 | B. | 6 | C. | $2\sqrt{3}$ | D. | 3 |
3.函数y=sin2x+cos2x如何平移可以得到函数y=sin2x-cos2x图象( )
| A. | 向左平移$\frac{π}{2}$ | B. | 向右平移$\frac{π}{2}$ | C. | 向左平移$\frac{π}{4}$ | D. | 向右平移$\frac{π}{4}$ |
1.已知实数x,y满足约束条件$\left\{{\begin{array}{l}{x+y+1≥0}\\{{x^2}+{y^2}≤4}\\{xy≥0}\end{array}}\right.$,则z=2x+y的取值范围是( )
| A. | $[-2,2\sqrt{5}]$ | B. | [-2,0] | C. | $[-2\sqrt{5},2]$ | D. | $[\frac{{2\sqrt{5}}}{5},1]$ |
 如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.
如图,在四棱锥P-ABCD中,PA⊥平面ABCD,AD∥BC,AD⊥CD,且AD=CD=2$\sqrt{2}$,PA=2,BC=4$\sqrt{2}$.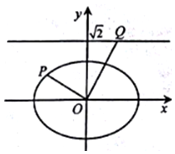 如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.
如图,在平面直角坐标系xOy中,已知椭圆$\frac{x^2}{a^2}+\frac{y^2}{b^2}=1$(a>b>0)的离心率为$\frac{{\sqrt{2}}}{2}$,右焦点到直线x=$\frac{a^2}{c}$的距离为1.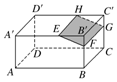 如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.
如图,长方体ABCD-A'B'C'D'被截去一部分,其中EH∥A'D',截去的几何体是三棱柱,则剩下的几何体是五棱柱.