题目内容
14.同时具有性质:①最小正周期是π;
②图象关于直线x=$\frac{π}{3}$对称;
③在区间$[{\frac{5π}{6},π}]$上是单调递增函数”的一个函数可以是( )
| A. | $y=cos(\frac{x}{2}+\frac{π}{6})$ | B. | $y=sin(2x+\frac{5π}{6})$ | C. | $y=cos(2x-\frac{π}{3})$ | D. | $y=sin(2x-\frac{π}{6})$ |
分析 利用正弦函数、余弦函数的图象和性质,逐一检验,可得结论.
解答 解:对于y=cos($\frac{x}{2}$+$\frac{π}{6}$),它的周期为$\frac{2π}{\frac{1}{2}}$=4π,故不满足条件.
对于y=sin(2x+$\frac{5π}{6}$),在区间$[{\frac{5π}{6},π}]$上,2x+$\frac{5π}{6}$∈[$\frac{5π}{2}$,$\frac{17π}{6}$],故该函数在区间$[{\frac{5π}{6},π}]$上不是单调递增函数,故不满足条件.
对于y=cos(2x-$\frac{π}{3}$),当x=$\frac{π}{3}$时,函数y=$\frac{1}{2}$,不是最值,故不满足②它的图象关于直线x=$\frac{π}{3}$对称,故不满足条件.
对于y=sin(2x-$\frac{π}{6}$),它的周期为$\frac{2π}{2}$=π,当x=$\frac{π}{3}$时,函数y=1,是函数的最大值,满足它的图象关于直线x=$\frac{π}{3}$对称;
且在区间$[{\frac{5π}{6},π}]$上,2x-$\frac{π}{6}$∈[$\frac{3π}{2}$,$\frac{11π}{6}$],故该函数在区间$[{\frac{5π}{6},π}]$上是单调递增函数,满足条件.
故选:D.
点评 本题主要考查正弦函数、余弦函数的图象和性质,属于基础题.

练习册系列答案
相关题目
5. 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
 如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )
如图,将抛物线C1:y=$\frac{1}{2}$x2+2x沿x轴对称后,向右平移3个单位,再向下平移5个单位,得到抛物线C2,若抛物线C1的顶点为A,点P是抛物线C2上一点,则△POA的面积的最小值为( )| A. | 3 | B. | 3.5 | C. | 4 | D. | 4.5 |
19.已知f(x)=x2+2x,则f′(2)=( )
| A. | 2 | B. | 4 | C. | 6 | D. | 8 |
4.设函数f(x)=sin(2x+α)+$\sqrt{3}$cos(2x+α)(0<α<$\frac{π}{2}$),且图象关于直线x=$\frac{π}{24}$对称,则( )
| A. | 函数f(x)的周期为π,且在区间[$\frac{π}{3}$,π]内单调递增 | |
| B. | 函数f(x)的周期为π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| C. | 函数f(x)的周期为2π,且在区间[$\frac{2π}{3}$,π]内单调递增 | |
| D. | 函数f(x)的周期为$\frac{π}{2}$,且在区间[$\frac{π}{2}$,π]内单调递增 |
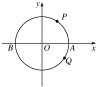 如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π.
如图,动点P,Q从点A(3,0)出发绕⊙O作圆周运动,若点M按逆时针方向每秒钟转$\frac{π}{3}$rad,点N按顺时针方向每秒钟转$\frac{π}{6}$rad.则当M、N第一次相遇时,点M转过的弧长为4π. 已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.
已知椭圆$\frac{{x}^{2}}{{a}^{2}}$+$\frac{{y}^{2}}{{b}^{2}}$=1(a>b>0)上顶点A(0,2),右焦点F(1,0),设椭圆上任一点到点M(0,6)的距离为d.