题目内容
已知椭圆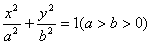 的长轴长为
的长轴长为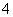 ,离心率为
,离心率为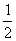 ,
,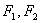 分别为其左右焦点.一动圆过点
分别为其左右焦点.一动圆过点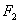 ,且与直线
,且与直线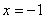 相切。
相切。
(Ⅰ) (ⅰ)求椭圆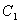 的方程; (ⅱ)求动圆圆心轨迹
的方程; (ⅱ)求动圆圆心轨迹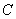 的方程;
的方程;
(Ⅱ) 在曲线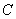 上有两点
上有两点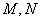 ,椭圆
,椭圆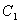 上有两点
上有两点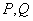 ,满足
,满足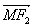 与
与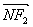 共线,
共线,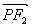 与
与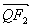 共线,且
共线,且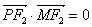 ,求四边形
,求四边形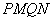 面积的最小值。
面积的最小值。
解:(Ⅰ)(ⅰ)由已知可得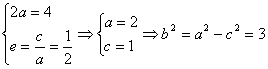 ,
,
则所求椭圆方程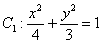 . …………3分
. …………3分
(ⅱ)由已知可得动圆圆心轨迹为抛物线,且抛物线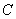 的焦点为
的焦点为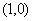 ,准线方程为
,准线方程为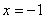 ,则动圆圆心轨迹方程为
,则动圆圆心轨迹方程为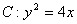 . …………6分
. …………6分
(Ⅱ)当直线MN的斜率不存在时,|MN|=4,此时PQ的长即为椭圆长轴长,|PQ|=4,
从而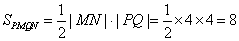 . …………8分
. …………8分
设直线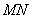 的斜率为
的斜率为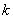 ,则
,则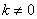 ,直线
,直线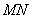 的方程为:
的方程为: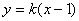 直线PQ的方程为
直线PQ的方程为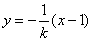 ,
,
设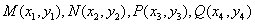
由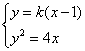 ,消去
,消去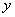 可得
可得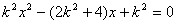 …………9分
…………9分
由抛物线定义可知: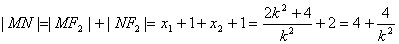
由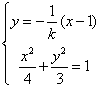 ,消去
,消去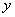 得
得 ,…………10分
,…………10分
从而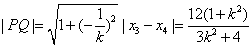 ,
,
∴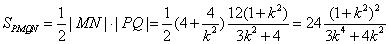 …………11分
…………11分
令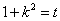 ,∵k>0,则
,∵k>0,则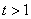 则
则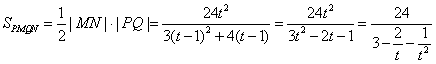
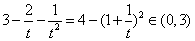 …………12分
…………12分
所以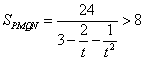 所以四边形
所以四边形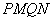 面积的最小值为8.
面积的最小值为8.
的最后一步另解: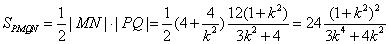
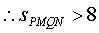

练习册系列答案
相关题目
 满足:
满足: ;则
;则 ( )
( )







 ,则“
,则“ 且
且 ”是“点
”是“点 在直线
在直线 上”的 ( )
上”的 ( ) 为平面内两定点,过该平面内动点
为平面内两定点,过该平面内动点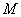 作直线
作直线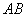 的垂线,垂足为
的垂线,垂足为 .若
.若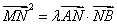 ,其中
,其中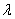 为常数,则动点
为常数,则动点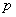 :对任意实数
:对任意实数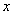 ,不等式
,不等式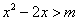 恒成立;命题
恒成立;命题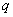 :方程
:方程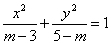 表示焦点在
表示焦点在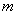 的取值范围;
的取值范围;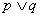 ”为真命题,且“
”为真命题,且“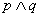 ”为假命题,求实数
”为假命题,求实数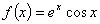 的图象在点
的图象在点 处的切线的倾斜角为( )
处的切线的倾斜角为( )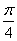 B.0 C.
B.0 C.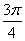 D.1
D.1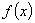 满足
满足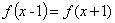 ,且在
,且在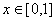 时,
时, 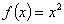 ,
,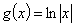 ,
,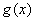 图象交点的个数是 .
图象交点的个数是 . ,则目标函数
,则目标函数 的取值范围是( )
的取值范围是( )  ,2] D.[2,6]
,2] D.[2,6] }中,已知
}中,已知
 ,则n为 ( )
,则n为 ( )