题目内容
10.设f(x)为奇函数,且当x>0,f(x)=x(1+$\root{3}{x}$).(1)求f(1),f(-2)的值;
(2)求f(x)在R上的表达式.
分析 (1)根据函数奇偶性的性质,即可求f(1),f(-2)的值;
(2)利用奇函数的对称性即可求f(x)在R上的表达式.
解答 解:(1)∵f(x)为奇函数,且当x>0,f(x)=x(1+$\root{3}{x}$).
∴f(1)=1+1=2,
f(-2)=-f(2)=-2×$(1+\root{3}{2})$=-2+2•$\root{3}{2}$;
(2)∵f(x)为奇函数,且当x>0,f(x)=x(1+$\root{3}{x}$).
∴f(0)=0,
当x<0,则-x>0,则f(-x)=-x(1-$\root{3}{x}$)=-f(x),
即f(x)=x(1-$\root{3}{x}$),
即f(x)在R上的表达式为f(x)=$\left\{\begin{array}{l}{x(1+\root{3}{x}),}&{x≥0}\\{x(1-\root{3}{x}),}&{x<0}\end{array}\right.$.
点评 本题主要考查函数解析式的求解以及函数值的计算,利用函数奇偶性的性质进行转化是解决本题的关键.

练习册系列答案
 举一反三同步巧讲精练系列答案
举一反三同步巧讲精练系列答案 口算与应用题卡系列答案
口算与应用题卡系列答案 名师点睛字词句段篇系列答案
名师点睛字词句段篇系列答案
相关题目
1.如图所示,在正面体ABCD-A1B1C1D1中,AD1∩A1D=O,则线段CO在平面AD1内的射影是( )
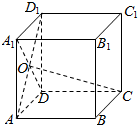

| A. | 线段DO | B. | 线段D1O | C. | 线段A1O | D. | 线段AO |
18.若AB∥A′B′,AC∥A′C′,则有( )
| A. | ∠BAC=∠B′A′C′ | |
| B. | ∠BAC+∠B′A′C′=180° | |
| C. | ∠BAC=∠B′A′C′或∠BAC+∠B′A′C′=180° | |
| D. | ∠BAC>∠B′A′C′ |
15.函数f(x)=$\sqrt{{x}^{2}}$是( )
| A. | 偶函数 | B. | 奇函数 | ||
| C. | 非奇非偶函数 | D. | 既是奇函数又是偶函数 |