题目内容
20.已知函数f(x)=|x+2a|+|x-$\frac{1}{{a}^{2}}$|.(1)当a=1时.求不等式f(x)≤9的解集:
(2)若不等式f(x)≥m对任意实数x和任意正实数a恒成立.求m的取值范围.
分析 (1)由条件利用绝对值的几何意义,求得不等式的解集.
(2)由条件利用绝对值三角不等式,求得函数f(x)的最小值,可得m的范围.
解答 解:(1)当a=1时.求不等式f(x)≤9,即|x+2|+|x-1|≤9.
而|x+2|+|x-1|表示上轴上的x对应点到-2、1对应点的距离之和,而-5和4对应点到-2、1对应点的距离之和正好等于9,
故|x+2|+|x-1|≤9的解集为[-5,4].
(2)若不等式f(x)≥m对任意实数x和任意正实数a恒成立,故m≤f(x)min.
∵f(x)=|x+2a|+|x-$\frac{1}{{a}^{2}}$|≥|x+2a-(x-$\frac{1}{{a}^{2}}$)|=|2a+$\frac{1}{{a}^{2}}$|=|a+a+$\frac{1}{{a}^{2}}$|=|a|+|a|+|$\frac{1}{{a}^{2}}$|≥3,
∴m≤3.
点评 本题主要考查绝对值的意义,绝对值不等式的性质以及解法,绝对值三角不等式,属于中档题.

练习册系列答案
相关题目
5.某几何体的三视图如图所示,则该几何体的体积为( )


| A. | 16-π | B. | 8+π | C. | 16+π | D. | 8-π |
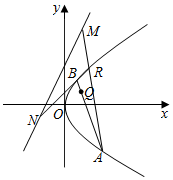 已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.
已知抛物线C的方程为y2=2px(p>0),抛物线的焦点到直线l:y=2x+2的距离为$\frac{4\sqrt{5}}{5}$.