题目内容
若集合A={x|-2＜x＜1}，B={x|0＜x＜1}，则集合A∩B=（ ）
| A、{x|-1＜x＜1} |
| B、{x|-2＜x＜1} |
| C、{x|-2＜x＜2} |
| D、{x|0＜x＜1} |
考点：交集及其运算
专题：集合
分析：利用交集的性质求解．
解答：
解：∵集合A={x|-2＜x＜1}，B={x|0＜x＜1}，
∴集合A∩B={x|0＜x＜1}．
故选：D．
∴集合A∩B={x|0＜x＜1}．
故选：D．
点评：本题考查交集的求法，是基础题，解题时要认真审题，注意交集和不等式性质的合理运用．
练习册系列答案
相关题目
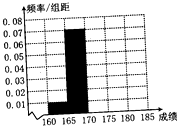某校在自主招生考试成绩中随机抽取100名学生的笔试成绩，被抽取学生的成绩均不低于160分，且低于185分，如图是按成绩分组得到的频率分布图的一部分（每一组均包括左端点数据），且第三组、第四组、第五组的频数之比一次为3：2：1．函数y=
•
的定义域为（ ）
| x-2 |
| x+5 |
| A、[一5，2] |
| B、（一∞，-5]U[2，+oo） |
| C、[一5，+∞） |
| D、[2，+∞） |
设集合A={1，2，3，4，5}，B={y|y=2x，x∈A}，则A∩B=（ ）
| A、{1，2，3，4，5} |
| B、{1，2，3，4，5，6，8，10} |
| C、{2，4} |
| D、∅ |
已知集合A={x|x≤1}，B={x|x2-2x＜0}．则A∩B=（ ）
| A、（0，1] |
| B、[1，2） |
| C、（0，1） |
| D、（0，2） |