Question

19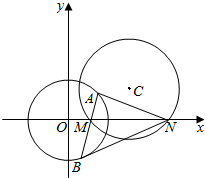．如图，圆C：x²-（1+a）x+y²-ay+a=0．
（1）若圆C的半径为$\frac{1}{2}$，求圆C的方程；
（2）已知a＞1，圆C与x轴相交于两点M，N（点M在点N的左侧）．过点M任作一条直线与圆O：x²+y²=4相交于两点A，B．问：是否存在实数a，使得∠ANM=∠BNM？若存在，求出实数a的值，若不存在，请说明理由．

Answer 1

分析 （1）由r=$\frac{1}{2}\sqrt{{D}^{2}+{E}^{2}-4F}$，得$\frac{1}{2}\sqrt{（1+a）^{2}+{a}^{2}-4a}$=$\frac{1}{2}$，由此求得a的值，从而求得所求圆C的方程．
（2）先求出所以M（1，0），N（a，0），假设存在实数a，当直线AB与x轴不垂直时，设直线AB的方程为y=k（x-1），代入x²+y²=4，利用韦达定理，根据NA、NB的斜率之和等于零求得a的值．经过检验，当直线AB与x轴垂直时，这个a值仍然满足∠ANM=∠BNM，从而得出结论．

解答 解：（1）由r=$\frac{1}{2}\sqrt{{D}^{2}+{E}^{2}-4F}$
得$\frac{1}{2}\sqrt{（1+a）^{2}+{a}^{2}-4a}$=$\frac{1}{2}$，
所以a=1或a=0，
故所求圆C的方程为x²-2x+y²-y+1=0或x²-x+y²=0；
（2）令y=0，得x²-（1+a）x+a=0，即（x-1）（x-a）=0，求得x=1，或x=a，
所以M（1，0），N（a，0）．
假设存在实数a，当直线AB与x轴不垂直时，设直线AB的方程为y=k（x-1），
代入x²+y²=4得，（1+k²）x²-2k²x+k²-4=0，
设A（x₁，y₁），B（x₂，y₂），从而x₁+x₂=$\frac{2{k}^{2}}{1+{k}^{2}}$，x₁x₂=$\frac{{k}^{2}-4}{1+{k}^{2}}$．
因为NA、NB的斜率之和为$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=$\frac{k[（{x}_{1}-1）（{x}_{2}-a）+（{x}_{2}-1）（{x}_{1}-a）]}{（{x}_{1}-a）（{x}_{2}-a）}$，
而（x₁-1）（x₂-a）+（x₂-1）（x₁-a）=2x₁x₂-（a+1）（x₂+x₁）+2a=$\frac{2a-8}{1+{k}^{2}}$，
因为∠ANM=∠BNM，所以，NA、NB的斜率互为相反数，$\frac{{y}_{1}}{{x}_{1}-a}$+$\frac{{y}_{2}}{{x}_{2}-a}$=0，即$\frac{2a-8}{1+{k}^{2}}$=0，得a=4．
当直线AB与x轴垂直时，仍然满足∠ANM=∠BNM，即NA、NB的斜率互为相反数．
综上，存在a=4，使得∠ANM=∠BNM．

点评 本题主要考查求圆的标准方程，直线和圆的位置关系，直线的倾斜角和斜率，属于中档题．