题目内容
若满足∠ABC=
,AC=1,BC=t的△ABC恰有一个,则实数t的取值范围是 .
| π |
| 4 |
考点:正弦定理
专题:解三角形
分析:先通过正弦定理用sinA表示出t,进而根据已知条件推断出A的范围,则t的范围可得.
解答:
解:由正弦定理知
=
,
∴sinA=
•BC=
t,
若△ABC恰有一个,则需要三角形为直角三角形或为钝角三角形,若C为钝角或直角,
则
<A+
≤
,0<A≤
,
t=
sinA,
0<则t≤1
若A为直角即A=
,
t=
sinA,t=
,
故答案为:(0,1]∪{
}.
| AC |
| sinB |
| BC |
| sinA |
∴sinA=
| sinB |
| AC |
| ||
| 2 |
若△ABC恰有一个,则需要三角形为直角三角形或为钝角三角形,若C为钝角或直角,
则
| π |
| 4 |
| π |
| 4 |
| π |
| 2 |
| π |
| 4 |
t=
| 2 |
0<则t≤1
若A为直角即A=
| π |
| 2 |
t=
| 2 |
| 2 |
故答案为:(0,1]∪{
| 2 |
点评:本题主要考查了正弦定理的运用.解题的过程中对另外两个角综合考虑.

练习册系列答案
 全优点练单元计划系列答案
全优点练单元计划系列答案
相关题目
已知cosα=-
,α∈(
,π),则cos(
+α)=( )
| 4 |
| 5 |
| π |
| 2 |
| π |
| 2 |
A、-
| ||
B、
| ||
C、-
| ||
D、
|
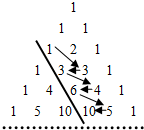 如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为
如图,在杨辉三角中,斜线l的上方从1按箭头方向可以构成一个“锯齿形”的数列{an}:1,3,3,4,6,5,10,…,记其前n项和为Sn,则S27的值为