题目内容
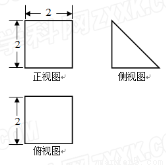
(本小题满分14分)三棱柱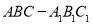 的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示,
的直观图及三视图(正视图和俯视图是正方形,侧视图是等腰直角三角形)如图所示, 为
为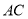 的中点.
的中点.
(1)求证: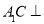 平面
平面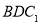 ;
;
(2)求二面角 的正切值.
的正切值.
(1)证明详见解析;(2) .
.
【解析】
试题分析:本题主要考查三视图、线线垂直、线面垂直、空间向量法、补体法等基础知识,考查学生的分析问题解决问题的能力、空间想象能力、逻辑推理能力、转化能力、计算能力. 第一问,利用线面垂直的性质,得到 ,再由
,再由 ,利用线面垂直的判定,得到
,利用线面垂直的判定,得到 平面
平面 ,利用线面垂直的性质得
,利用线面垂直的性质得 ,再由
,再由 、
、 ,利用线面垂直的判定,得到
,利用线面垂直的判定,得到 平面
平面 ,
,
 平面
平面 ,
, 平面
平面 ;第二问,利用空间向量法,建立空间直角坐标系,得到
;第二问,利用空间向量法,建立空间直角坐标系,得到 和
和 向量的坐标,计算出平面
向量的坐标,计算出平面 和平面
和平面 的法向量,再利用夹角公式得到
的法向量,再利用夹角公式得到 ,最后再计算
,最后再计算 .
.
试题解析:由三视图可知,几何体为直三棱柱 —
— ,侧面
,侧面 为边长为2的正方形,底面
为边长为2的正方形,底面 是等腰直角三角形,
是等腰直角三角形, 2分
2分
(1)直三棱柱 —
— 中,
中, 平面
平面 ,
, 平面
平面 ,
,
 ,
, ,D为AC的中点,
,D为AC的中点, ,
,
又 面
面 ,
, 面
面 ,且
,且
 ,
,
 平面
平面 ,又
,又 面
面 ,
, ① ..6分
① ..6分
 又
又 ,
,
又 面
面 ,
, 面
面 ,且
,且
 ,
,
 面
面 ,
, 面
面 ,
,

在正方形 中,
中,
又 面
面 ,
, 面
面 ,且
,且
 ,
,
 面
面 ,又
,又 面
面 ,
,
 ② ..8分
② ..8分
由①②,又 面
面 ,
, 面
面 ,且
,且
 ,
,
 面
面 . 9分
. 9分

(2)解法一(空间向量法)以 为原点建系,易得
为原点建系,易得
设平面 的法向量
的法向量 由
由 ,
,
得 令
令 ,得
,得 ..12分
..12分
又平面 的法向量
的法向量 设二面角
设二面角 的平面角为
的平面角为 ,
,
所以 ..14分
..14分
解法二:

所求二面角 与二面角
与二面角 互余,
互余,
取 中点
中点 ,有
,有 ⊥平面
⊥平面 ,过
,过 作
作 垂线,垂足为
垂线,垂足为 ,
,


所以二面角 的平面角是
的平面角是 11分
11分
 ,
,
因为二面角 与二面角
与二面角 互余,
互余,
所以二面角 的正切值为
的正切值为 ; ..14分
; ..14分
解法三(补形)如图补成正方体,易得 为二面角的平面角,
为二面角的平面角,
 ..14分
..14分

考点:三视图、线线垂直、线面垂直、空间向量法、补体法.

练习册系列答案
相关题目
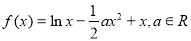
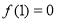 ,求函数
,求函数  的单调递减区间;
的单调递减区间;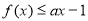 恒成立,求整数 a的最小值:
恒成立,求整数 a的最小值: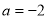 ,正实数
,正实数 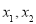 满足
满足 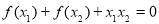 ,证明:
,证明: 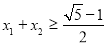


 (i是虚数单位),则
(i是虚数单位),则 的取值范围是( )
的取值范围是( ) B.(1,5) C.(1,3) D.
B.(1,5) C.(1,3) D.
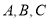 是平面内不共线的三点,点P在该平面内且有
是平面内不共线的三点,点P在该平面内且有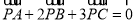 ,现将一粒黄豆随机撒在△
,现将一粒黄豆随机撒在△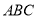 内,则这粒黄豆落在△
内,则这粒黄豆落在△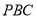 内的概率为__________.
内的概率为__________. ,则
,则 ______.
______. 中,
中,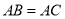 ,
,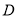 在线段
在线段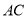 ,
,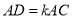 (
(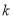 为常数,且
为常数,且 ),
), 为定长,则
为定长,则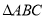 的面积最大值为( )
的面积最大值为( ) B.
B. C.
C.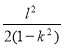 D.
D.