题目内容
18．一等腰三角形的两边长分别为3和6，则其底角的余弦为$\frac{1}{4}$．分析 可分3为腰长和底边长两种情况，求得直角三角形中底角的邻边与斜边之比即可．
解答 解：①当腰长为3时，底边长为6，则3+3=6，由三角形两边之和大于第三边可知无解．
②当底边为3时，作AD⊥BC于D．
同理可得BD=CD=$\frac{3}{2}$，
∴cosB=$\frac{\frac{3}{2}}{6}$=$\frac{1}{4}$．
故答案为：$\frac{1}{4}$．
点评 考查锐角三角函数的知识；掌握一个角的余弦值的求法是解决本题的关键；分情况探讨是解决本题的易错点．
练习册系列答案
小学课时作业全通练案系列答案
金版课堂课时训练系列答案
单元全能练考卷系列答案
新黄冈兵法密卷系列答案
相关题目
8．将函数f（x）=$\sqrt{3}$sinωx+cosωx（ω＞0）的图象向右平移$\frac{π}{4}$个单位，得到函数g（x）的图象，函数g（x）的相邻的两个极值点的距离等于$\frac{π}{2}$，则g（x）的单调递减区间是（ ）
| A． | [kπ+$\frac{5π}{12}$，kπ+$\frac{11π}{12}$]，k∈Z | B． | [kπ+$\frac{π}{12}$，kπ+$\frac{5π}{12}$]，k∈Z | ||
| C． | [2kπ+$\frac{5π}{12}$，2kπ+$\frac{11π}{12}$]，k∈Z | D． | [2kπ-$\frac{π}{12}$，2kπ+$\frac{5π}{12}$]，k∈Z |
9．若$\root{n}{a}$=-$\root{n}{a}$，则（ ）
| A． | a=0 | B． | a≠0 | C． | a≤0 | D． | a≥0 |
，条件
，且
是
的一个必要不充分条件，求实数
的取值范围．
在点
处的切线的斜率是 ．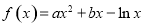
（
）．
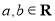时，求函数
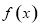在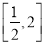
上的最大值和最小值；
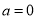时，是否存在正实数
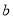，当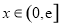
（
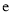是自然对数底数）时，函数
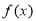的最小值是3，若存在，求出