题目内容
7.已知向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(1,-1),则$\overrightarrow{a}$•(2$\overrightarrow{b}-\overrightarrow{a}$)=-24.分析 根据平面向量的坐标运算与数量积的定义计算即可.
解答 解:向量$\overrightarrow{a}$=(2,4),$\overrightarrow{b}$=(1,-1),
∴2$\overrightarrow{b}-\overrightarrow{a}$=(0,-6),
∴$\overrightarrow{a}$•(2$\overrightarrow{b}-\overrightarrow{a}$)=2×0+4×(-6)=-24.
故答案为:-24.
点评 本题考查了平面向量的坐标运算与数量积运算,是基础题目.

练习册系列答案
 小学教材全测系列答案
小学教材全测系列答案 小学数学口算题卡脱口而出系列答案
小学数学口算题卡脱口而出系列答案 优秀生应用题卡口算天天练系列答案
优秀生应用题卡口算天天练系列答案 浙江之星课时优化作业系列答案
浙江之星课时优化作业系列答案
相关题目
15.若b<a<0,则下列不等式一定成立的是( )
| A. | a3<b3 | B. | ab>b2 | C. | ac2>bc2 | D. | $\frac{1}{a}$<$\frac{1}{b}$ |
2.某用水量较大的企业为积极响应政府号召的“节约用水,我们共同的责任”的倡议,对生产设备进行技术改造,下表提供了该企业节约用水技术改造后生产甲产品过程中记录的产量x(吨)与相应的生产用水y(吨)的几组对照数据:
(1)若x,y之间是线性相关,请根据表中提供的数据,求y关于x的线性回归方程y=bx+a;
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
| x | 1 | 2 | 3 | 4 |
| y | 0.4 | 0.9 | 1.1 | 1.6 |
(2)已知该厂技术改造前100吨甲产品的生产用水为120吨,试根据(1)中求出的线性回归方程,预测技术改造后生产100吨甲产品的用水量比技术改造前减少了多少吨?
(参考公式:$\widehat{b}$=$\frac{\sum_{i=1}^{n}{x}_{i}{y}_{1}-n\overline{x}\overline{y}}{\sum_{i=1}^{n}{x}_{i}^{2}-n\stackrel{-2}{x}}$,$\widehat{a}$=$\overline{y}$-$\widehat{b}$$\overline{x}$)
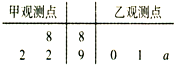 如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.
如图,茎叶图记录了某城市甲、乙两个观测点连续三天观测到的空气质量指数(AQI).乙观测点记录中有一个数字模糊无法确认,已知该数是0,1,…,9中随机的一个数,并在图中以a表示.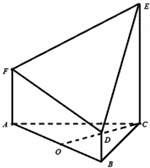 如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.
如图所示的几何体是由等边三角形ABC的底面的棱柱被平面DEF所截得,已知FA⊥平面ABC,AB=2,BD=1,AF=2,CE=3,O为AB的中点.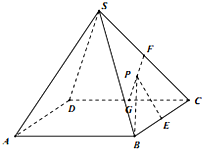 如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.
如图,正四棱锥S-ABCD中.SA=AB=2,E、F、G分别为BC、SC、DC的中点,设P为线段FG上任意一点.