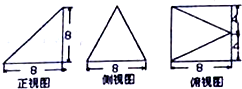
题目内容
若把函数f(x)=ln(2x+4)图象向右平移2个单位得新函数y=g(x),再把y=g(x)的图象绕原点O逆时针旋转角α后恰与y轴相切,则tanα= .
考点:函数的图象与图象变化
专题:函数的性质及应用,导数的综合应用
分析:本题可先将函数图象进行平移,再求出其过原点的切线方程,然后根据题意,对所得曲线进行整体(含切线)的旋转后,切线与y轴重合时(所得曲线与y轴相切),求出旋转前的切线与y轴所成角的正切,即得到本题的解.
解答:
解:将函数f(x)=ln(2x+4)图象向右平移2个单位得新函数y=ln[2(x-2)+4]=ln2x,
∴g(x)=ln2x.
g′(x)=
.
过原点作曲线y=g(x)的切线,设切点为P(x0,y0),
则有:y0=ln2x0,斜率k=
,
∴切线方程为:y-ln2x0=
(x-x0),
切线过原点时,x=0,y=0,
∴ln2x0=1,x0=
.
由题意知,y=g(x)的切线与y轴的夹角为α,
则tan(
-α)=
=
,tanα=
.
故答案为:
.
∴g(x)=ln2x.
g′(x)=
| 1 |
| x |
过原点作曲线y=g(x)的切线,设切点为P(x0,y0),
则有:y0=ln2x0,斜率k=
| 1 |
| x0 |
∴切线方程为:y-ln2x0=
| 1 |
| x0 |
切线过原点时,x=0,y=0,
∴ln2x0=1,x0=
| e |
| 2 |
由题意知,y=g(x)的切线与y轴的夹角为α,
则tan(
| π |
| 2 |
| 1 |
| x0 |
| 2 |
| e |
| e |
| 2 |
故答案为:
| e |
| 2 |
点评:本题考查了函数图象的平移、旋转和切线方程等知识,利用函数图象平移和旋转,实现图象与y轴的相切,思维上有一定的跨度,属于中档题.

练习册系列答案
 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案
相关题目