题目内容
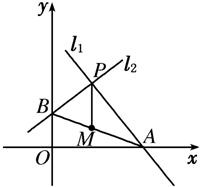
过点P(1,1)且互相垂直的两条直线l1与l2分别与x,y轴交于A,B两点,则AB中点M的轨迹方程为 .
考点:轨迹方程
专题:计算题,直线与圆
分析:设M的坐标为(x,y),欲求线段AB的中点M的轨迹方程,只须求出坐标x,y的关系式即可,由题意得|PM|=|OM|,利用两点间的距离公式将点的坐标代入后化简即得M的轨迹方程.
解答:
 解:设M的坐标为(x,y),
解:设M的坐标为(x,y),
则A、B两点的坐标分别是(2x,0),(0,2y),连接PM,
∵l1⊥l2,∴|PM|=|OM|.
而|PM|=
,
|OM|=
∴
=
,
化简,得x+y-1=0即为所求的轨迹方程.
故答案为:x+y-1=0.
 解:设M的坐标为(x,y),
解:设M的坐标为(x,y),则A、B两点的坐标分别是(2x,0),(0,2y),连接PM,
∵l1⊥l2,∴|PM|=|OM|.
而|PM|=
| (x-1)2+(y-1)2 |
|OM|=
| x2+y2 |
∴
| (x-1)2+(y-1)2 |
| x2+y2 |
化简,得x+y-1=0即为所求的轨迹方程.
故答案为:x+y-1=0.
点评:本题主要考查了轨迹方程、两条直线垂直与倾斜角、斜率的关系等知识,属于中档题.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目
若点(a,4)在函数y=2x的图象上,则tan
的值为( )
| aπ |
| 6 |
| A、0 | ||||
B、
| ||||
| C、1 | ||||
D、
|
已知y=sin30°,则导数y′=( )
A、
| ||||
B、-
| ||||
C、
| ||||
| D、0 |
把函数y=sin(2x-
)的图象向左平移
个单位,所得图象的函数是( )
| π |
| 4 |
| π |
| 8 |
| A、最小正周期为π的奇函数 |
| B、最小正周期为π的偶函数 |
| C、最小正周期为2π的奇函数 |
| D、最小正周期为2π的偶函数 |